题目内容
4.已知抛物线x2=4$\sqrt{3}$y的准线过双曲线$\frac{{x}^{2}}{{m}^{2}}$-y2=-1的焦点,则双曲线的离心率为( )| A. | $\frac{3\sqrt{2}}{4}$ | B. | $\frac{3\sqrt{10}}{4}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 由抛物线x2=4$\sqrt{3}$y得准线方程为y=-$\sqrt{3}$,因此双曲线的一个焦点和c,再利用离心率计算公式即可得出.
解答 解:由抛物线x2=4$\sqrt{3}$y得准线方程为y=-$\sqrt{3}$,因此双曲线的一个焦点为(0,-$\sqrt{3}$),∴c=$\sqrt{3}$.
双曲线$\frac{{x}^{2}}{{m}^{2}}$-y2=-1化为y2-$\frac{{x}^{2}}{{m}^{2}}$-=-1,
∴a=1,
∴双曲线的离心率e=$\frac{c}{a}$=$\sqrt{3}$.
故选:C.
点评 本题考查了圆锥曲线的标准方程及其性质,属于基础题.

练习册系列答案
相关题目
2.函数f(x)=ax3-3x+1,对于x∈[-1,1]总有f(x)≥0成立,则a的取值集合为( )
| A. | (-∞,0] | B. | [2,4] | C. | [4,+∞) | D. | {4} |
3.|a-b|=|a|+|b|成立的条件是( )
| A. | ab>0 | B. | ab>1 | C. | ab≤0 | D. | ab≤1 |
12.已知定义在R上的函数f(x)满足f(x+1.5)=-f(x),当x∈[0,3)时,f(x)=|(x-1)2-0.5|,记集合A={n|n是函数y=f(x)(-3≤x≤5.5)的图象与直线y=m(m∈R)的交点个数},则集合A的子集个数为( )
| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
14.为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
(Ⅰ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段居民的休闲方式与性别有关系”?
(Ⅱ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X.求X的数学期望和方差.
附:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1}+{n}_{2}+n+{1}^{n}+2}$.
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
(Ⅱ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X.求X的数学期望和方差.
| P(X2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
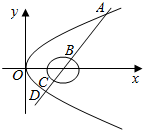 如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=14.
如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=14.