题目内容
曲线C：y=
x2+lnx+
上斜率最小的一条切线截圆x2+y2=1的弦长是 ．
【答案】分析：先对函数求导，然后利用基本不等式可求y′的最小值，进而可求切线方程，然后利用
即可求解
解答：解：对函数求导可得，
（x＞0）
∴y′≥2当且仅当x=1时取得最小值，此时切线方程是y-1=2（x-1）即2x-y-1=0
∵圆心（0，0）到直线2x-y-1=0的距离d=
∴直线截圆x2+y2=1的弦长为
=
故答案为：
点评：本题主要考查了导数的几何意义的应用，直线与圆相交性质的应用，解题的关键是利用公式
即可求解解答：解：对函数求导可得，
（x＞0）∴y′≥2当且仅当x=1时取得最小值，此时切线方程是y-1=2（x-1）即2x-y-1=0
∵圆心（0，0）到直线2x-y-1=0的距离d=
∴直线截圆x2+y2=1的弦长为
=故答案为：
点评：本题主要考查了导数的几何意义的应用，直线与圆相交性质的应用，解题的关键是利用公式
练习册系列答案
相关题目
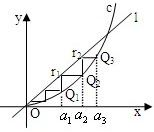设a＞0，如图，已知直线l：y=ax及曲线C：y=x2，C上的点Q1的横坐标为a1（0＜a1＜a）．从C上的点Qn（n≥1）作直线平行于x轴，交直线l于点Pn+1，再从点Pn+1作直线平行于y轴，交曲线C于点Qn+1．Qn（n=1，2，3，…）的横坐标构成数列{an}．
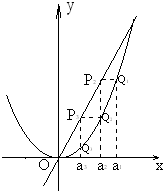（2013•广州三模）如图，已知直线l：y=4x及曲线C：y=x2，C上的点Q1的横坐标为a1（0＜a1＜4）．从曲线C上的点Qn（n≥1）作直线平行于x轴，交直线l于点Pn+1，再从点Pn+1作直线平行于y轴，交曲线C于点Qn+1．Qn（n=1，2，3，…）的横坐标构成数列{an}．