题目内容
已知2+ =22×
=22× ,3+
,3+ =33×
=33× ,4+
,4+ =44×
=44× ,…,若8+
,…,若8+ =88×
=88× (a、b为正整数),则a+b= .
(a、b为正整数),则a+b= .
【答案】分析:对几个等式加以观察,归纳当n=1、n=2和n=3时等式的特征,可得当n=k时的等式为:(k+1)+ ,将此规律按n=8代入,得
,将此规律按n=8代入,得  ,说明a+b=71.
,说明a+b=71.
解答:解:观察各个等式的特征,发现
第1个等式:(1+1)+
第2个等式:(2+1)+
第3个等式:(3+1)+
…
依此类推,得
第k个等式:(k+1)+
当k=8时,8+ =88×
=88× ,说明
,说明 ,说明a=8,b=63
,说明a=8,b=63
∴a+b=71
故答案为71.
点评:本题考查了数列的概念与简单表示法和归纳推理,属于中档题.抓住数列当中的规律,用函数的观点观察数列的特征面得出数列的通项,是解决本题的关键.
 ,将此规律按n=8代入,得
,将此规律按n=8代入,得  ,说明a+b=71.
,说明a+b=71.解答:解:观察各个等式的特征,发现
第1个等式:(1+1)+

第2个等式:(2+1)+

第3个等式:(3+1)+

…
依此类推,得
第k个等式:(k+1)+

当k=8时,8+
 =88×
=88× ,说明
,说明 ,说明a=8,b=63
,说明a=8,b=63∴a+b=71
故答案为71.
点评:本题考查了数列的概念与简单表示法和归纳推理,属于中档题.抓住数列当中的规律,用函数的观点观察数列的特征面得出数列的通项,是解决本题的关键.

练习册系列答案
相关题目
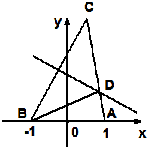 在平面直角坐标系中,点A(1,0)、B(-1,0),已知|CA|=2
在平面直角坐标系中,点A(1,0)、B(-1,0),已知|CA|=2 =22×
=22× =33×
=33× =44×
=44× =88×
=88×