题目内容
将等边三角形ABC沿中线AD对折使BD⊥AC，那么AB与平面ACD所成的角是
30度
30度
．分析：利用等边三角形的性质和线面垂直的判定定理可得BD⊥平面ACD．可得∠BAD是AB与平面ACD所成的角，求出即可．
解答：解：如图所示，
∵BD⊥DC，BD⊥AC，DC∩AC=C，
∴BD⊥平面ACD．
∴∠BAD是AB与平面ACD所成的角，
∵∠BAD=30°，∴AB与平面ACD所成的角是30°．
故答案为30°．
∵BD⊥DC，BD⊥AC，DC∩AC=C，
∴BD⊥平面ACD．
∴∠BAD是AB与平面ACD所成的角，
∵∠BAD=30°，∴AB与平面ACD所成的角是30°．
故答案为30°．
点评：熟练掌握等边三角形的性质和线面垂直的判定定理、线面角的定义等是解题的关键．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
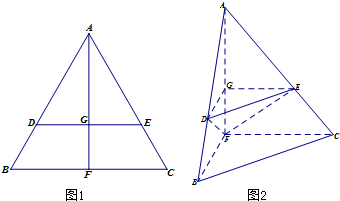（2013•广东）如图1，在边长为1的等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图2所示的三棱锥A-BCF，其中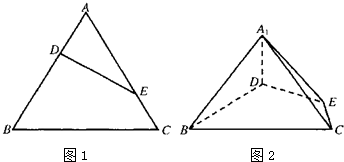
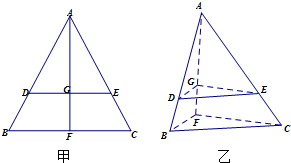如图甲，在等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC上的点，AF与DE交于点G，将△ABF沿AF折起，得到如图乙所示的三棱锥A-BCF，证明：DE∥平面BCF．