题目内容
已知曲线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 .
.
(1)将曲线 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)曲线 ,
, 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
(1) ;(2)
;(2) .
.
解析试题分析:(1)根据同角三角函数关系消去参数θ,即可求出曲线C1的普通方程,曲线C2的极坐标方程两边同乘ρ,根据极坐标公式进行化简就可求出直角坐标方程;(2)先求出两个圆心之间的距离与两半径和进行比较,设相交弦长为d,因为两圆半径相等,所以公共弦平分线段C1C2,建立等量关系,解之即可.
试题解析:解:(1)由 得
得
∴曲线 的普通方程为
的普通方程为
∵ ∴
∴
∵ ∴
∴ ,即
,即
∴曲线 的直角坐标方程为
的直角坐标方程为 5分
5分
(2)∵圆 的圆心为
的圆心为 ,圆
,圆 的圆心为
的圆心为
∴
∴两圆相交
设相交弦长为 ,因为两圆半径相等,所以公共弦平分线段
,因为两圆半径相等,所以公共弦平分线段
∴
∴ 10分.
10分.
考点:1.圆的参数方程;2.简单曲线的极坐标方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 、
、 、
、 是两两不等的实数,点
是两两不等的实数,点 ,
, ,点
,点 ,
, ,则直线
,则直线 的倾斜角为( )
的倾斜角为( )
A. | B.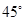 | C. | D. |
已知直线 与圆
与圆 有公共点, 且公共点的横坐标和纵坐标均为整数,
有公共点, 且公共点的横坐标和纵坐标均为整数,
那么这样的直线共有 ( )
| A.60条 | B.66条 | C.70条 | D.71条 |
如果输入 ,那么执行下图中算法后的输出结果是( )
,那么执行下图中算法后的输出结果是( )
A. | B. | C. | D. |
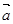
 ,向量
,向量 ,则
,则 方向上的投影为____.
方向上的投影为____. 的两条切线
的两条切线 和
和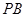 相交于点
相交于点 ,与⊙
,与⊙ 两点,
两点, 是⊙
是⊙ ,则
,则 ________.(用角度表示)
________.(用角度表示)
 画出输入自变量
画出输入自变量 的值求函数值y的程序框图
的值求函数值y的程序框图 ,则输出的结果是 .
,则输出的结果是 .
 ,
, 为
为 中点,则
中点,则 、
、