题目内容
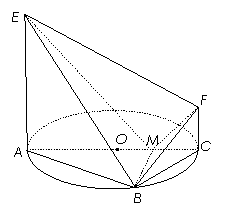
如图,![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 在圆
在圆![]() 上,
上,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
 |
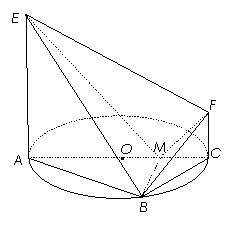
解:(1)![]() 平面
平面![]()
![]() 平面
平面![]() ,
, ![]() .……………1分
.……………1分
 |
又![]()
![]() ,
,
![]() 平面
平面![]()
而![]() 平面
平面![]()
![]() . ………………………………………3分
. ………………………………………3分
![]() 是圆
是圆![]() 的直径,
的直径,![]() .
.
又![]()
![]() ,
,
![]()
![]() .
.
![]() 平面
平面![]()
![]() ,
,![]() ,
,
![]() 平面
平面![]() .
.
![]()
![]() 与
与![]() 都是等腰直角三角形.
都是等腰直角三角形.
![]() .
.
![]() ,即
,即![]() (也可由勾股定理证得).………………………………5分
(也可由勾股定理证得).………………………………5分
![]() ,
, ![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,
,
![]()
![]() . ………………………………………………………………………………6分
. ………………………………………………………………………………6分
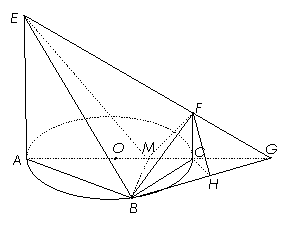
(2)延长![]() 交
交![]() 于
于![]() ,连
,连![]() ,过
,过![]() 作
作![]() ,连结
,连结![]() .
.
 |
由(1)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() .
.
而![]() ,
,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() ,
,
![]() 为平面
为平面![]() 与平面
与平面![]() 所成的
所成的
二面角的平面角. ……………………8分
在![]() 中,
中,![]()
![]() ,
,![]() ,
,
![]() .
.
由![]() ,得
,得![]() .
.
![]() .
.
又![]() ,
,
![]() ,则
,则![]() . ………………………………11分
. ………………………………11分
![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
![]() 平面
平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() . …12分
. …12分

练习册系列答案
相关题目
 是圆
是圆
 是圆
是圆 的直径,点
的直径,点 在圆
在圆 ,
, 交
交 ,
, 平面
平面 ,
, ,
, .
.
 ;
; 与平面
与平面 是圆
是圆 的直径,点
的直径,点 在圆
在圆 ,
, 交
交 ,
, 平面
平面 ,
, ,
, .
.
 ;
; 与平面
与平面 是圆
是圆 的直径,点
的直径,点 在圆
在圆 ,
, 交
交 ,
, 平面
平面 ,
, ,
, .
. ;
; 与平面
与平面
 是圆
是圆 的直径,点
的直径,点 在圆
在圆 ,
, 交
交 ,
, 平面
平面 ,
, ,
, .
.
 ;
; 与平面
与平面