题目内容
如图, 是圆
是圆 的直径,点
的直径,点 在圆
在圆 上,
上, ,
, 交
交 于点
于点 ,
, 平面
平面 ,
, ,
, .
.

(Ⅰ)证明: ;
;
(Ⅱ)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】
(Ⅰ)见解析(Ⅱ)
【解析】(1)根据线面垂直得到线与线垂直,根据直径所对的圆周角是直角,得到两个三角形是等腰直角三角形,有线面垂直得到结果.
(2)做出辅助线,延长EF交AC于G,连BG,过C作CH⊥BG,连接FH.,做出∠FHC为平面BEF与平面ABC所成的二面角的平面角,求出平面角.
解:(法一)(Ⅰ) 平面
平面
 平面
平面 ,
,  .……1分
.……1分
又
 ,
,
 平面
平面
而 平面
平面
 .………………3分
.………………3分
 是圆
是圆 的直径,
的直径, .
.
又
 ,
,

 .
.
 平面
平面
 ,
, ,
,
 平面
平面 .
.

 与
与 都是等腰直角三角形.
都是等腰直角三角形.
 .
.
 ,即
,即 (也可由勾股定理证得).…………………5分
(也可由勾股定理证得).…………………5分
 ,
,  平面
平面 .
.
而 平面
平面 ,
,

 . …………………………6分
. …………………………6分
(Ⅱ)延长 交
交 于
于 ,连
,连 ,过
,过 作
作 ,连结
,连结 .
.

由(1)知 平面
平面 ,
, 平面
平面 ,
,
 .
.
而 ,
, 平面
平面 .
.
 平面
平面 ,
,
 ,
,
 为平面
为平面 与平面
与平面 所成的
所成的
二面角的平面角. ……………………8分
在 中,
中,
 ,
, ,
,
 .
.
由 ,得
,得 .
.
 .
.
又 ,
,
 ,则
,则 .………………11分
.………………11分
 是等腰直角三角形,
是等腰直角三角形, .
.
 平面
平面 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为 .……………12分
.……………12分
(法二)(Ⅰ)同法一,得 .……………3分
.……………3分
如图,以 为坐标原点,垂直于
为坐标原点,垂直于 、
、 、
、 所在的直线为
所在的直线为 轴建立空间直角坐标系.
轴建立空间直角坐标系.

由已知条件得 ,
,
 . ………4分
. ………4分
由 ,
,
得 ,
,  . ……………6分
. ……………6分
(Ⅱ)由(1)知 .
.
设平面 的法向量为
的法向量为 ,
,
由 得
得 ,
,
令 得
得 ,
, ,………………9分
,………………9分
由已知 平面
平面 ,所以取面
,所以取面 的法向量为
的法向量为 ,
,
设平面 与平面
与平面 所成的锐二面角为
所成的锐二面角为 ,
,
则 ,……………11分
,……………11分
 平面
平面 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为 .………………12分
.………………12分

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 是圆
是圆
 是圆
是圆 的直径,点
的直径,点 在圆
在圆 ,
, 交
交 ,
, 平面
平面 ,
, ,
, .
.
 ;
; 与平面
与平面 是圆
是圆 的直径,点
的直径,点 在圆
在圆 ,
, 交
交 ,
, 平面
平面 ,
, ,
, .
. ;
; 与平面
与平面
 是圆
是圆 的直径,点
的直径,点 在圆
在圆 ,
, 交
交 ,
,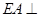 平面
平面 ,
, ,
, .
.
 ;
; 与平面
与平面