题目内容
(本题满分12分)如图, 是圆
是圆 的直径,点
的直径,点 在圆
在圆 上,
上, ,
, 交
交 于点
于点 ,
, 平面
平面 ,
, ,
, .
.

(1)证明: ;
;
(2)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】
(1)见解析;(2)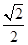 .
.
【解析】第一问证明几何中线线垂直,利用线面垂直的性质定理得到。由于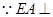 平面
平面
 平面
平面 ,
,
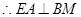
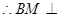 平面
平面
 在底面圆中利用圆的性质得到
在底面圆中利用圆的性质得到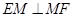 ,从而得到
,从而得到 平面
平面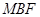 .
.
第二问中,通过作辅助线得到二面角的平面角的大小为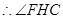 为平面
为平面 与平面
与平面 所成的二面角的平面角.然后借助于直角三角形求解得到结论。
所成的二面角的平面角.然后借助于直角三角形求解得到结论。
解:(法一)(1)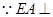 平面
平面
 平面
平面 ,
,
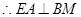 .……………1分
.……………1分
又
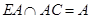 ,
,
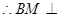 平面
平面
而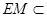 平面
平面
 . ………………………………………3分
. ………………………………………3分
 是圆
是圆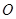 的直径,
的直径,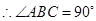 .
.
又
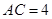 ,
,
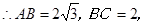
 .
.
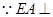 平面
平面
 ,
, ,
,
 平面
平面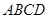 .
.
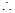
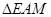 与
与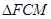 都是等腰直角三角形.
都是等腰直角三角形.
 .
.
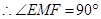 ,即
,即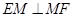 (也可由勾股定理证得).………………5分
(也可由勾股定理证得).………………5分
 ,
,  平面
平面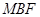 .
.
而 平面
平面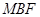 ,
,

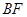 .
………………………………………………………………6分
.
………………………………………………………………6分
(2)延长 交
交 于
于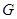 ,连
,连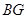 ,过
,过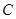 作
作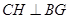 ,连结
,连结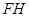 .
.
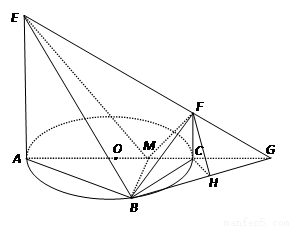
由(1)知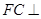 平面
平面 ,
,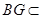 平面
平面 ,
,
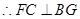 .
.
而 ,
, 平面
平面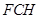 .
.
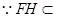 平面
平面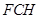 ,
,
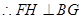 ,
,
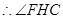 为平面
为平面 与平面
与平面 所成的
所成的
二面角的平面角. ……………………8分
在 中,
中,
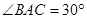 ,
,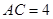 ,
,
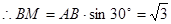 .
.
由 ,得
,得 .
.
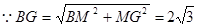 .
.
又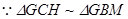 ,
,
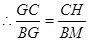 ,则
,则 . …………………11分
. …………………11分
 是等腰直角三角形,
是等腰直角三角形, .
.
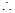 平面
平面 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为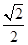 .
…………………12分
.
…………………12分
(法二)(1)同法一,得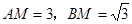 .
……………………3分
.
……………………3分
如图,以 为坐标原点,垂直于
为坐标原点,垂直于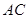 .
.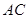 .
. 所在的直线为
所在的直线为 轴建立空间直角坐标系.
轴建立空间直角坐标系.

由已知条件得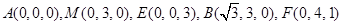 ,
,
 . ………4分
. ………4分
由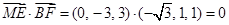 ,
,
得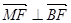 ,
,
 . ……………6分
. ……………6分
(2)由(1)知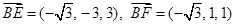 .
.
设平面 的法向量为
的法向量为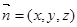 ,
,
由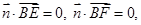 得
得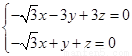 ,
,
令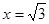 得
得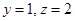 ,
,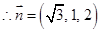 ,
………………9分
,
………………9分
由已知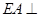 平面
平面 ,所以取面
,所以取面 的法向量为
的法向量为 ,
,
设平面 与平面
与平面 所成的锐二面角为
所成的锐二面角为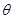 ,
,
则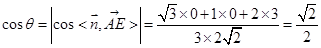 ,
…………………………11分
,
…………………………11分
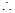 平面
平面 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为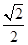 . ……………………12分
. ……………………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
