题目内容
函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移 个单位后,与函数y=sin(2x+
个单位后,与函数y=sin(2x+ )的图象重合,则φ= .
)的图象重合,则φ= .
【答案】分析:根据函数图象平移的公式,可得平移后的图象为y=cos[2(x-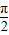 )+φ]的图象,即y=cos(2x+φ-π)的图象.结合题意得函数y=sin(2x+
)+φ]的图象,即y=cos(2x+φ-π)的图象.结合题意得函数y=sin(2x+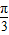 )=
)=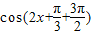 的图象与y=cos(2x+φ-π)图象重合,由此结合三角函数的诱导公式即可算出φ的值.
的图象与y=cos(2x+φ-π)图象重合,由此结合三角函数的诱导公式即可算出φ的值.
解答:解:函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移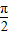 个单位后,得平移后的图象的函数解析式为
个单位后,得平移后的图象的函数解析式为
y=cos[2(x-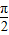 )+φ]=cos(2x+φ-π),
)+φ]=cos(2x+φ-π),
而函数y=sin(2x+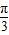 )=
)=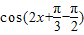 ,
,
由函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移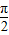 个单位后,与函数y=sin(2x+
个单位后,与函数y=sin(2x+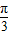 )的图象重合,得
)的图象重合,得
2x+φ-π=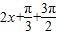 ,解得:x=
,解得:x=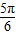 .
.
符合-π≤φ<π.
故答案为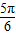 .
.
点评:本题给出函数y=cos(2x+φ)的图象平移,求参数φ的值.着重考查了函数图象平移的公式、三角函数的诱导公式和函数y=Asin(ωx+φ)的图象变换等知识,属于基础题.
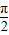 )+φ]的图象,即y=cos(2x+φ-π)的图象.结合题意得函数y=sin(2x+
)+φ]的图象,即y=cos(2x+φ-π)的图象.结合题意得函数y=sin(2x+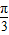 )=
)=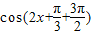 的图象与y=cos(2x+φ-π)图象重合,由此结合三角函数的诱导公式即可算出φ的值.
的图象与y=cos(2x+φ-π)图象重合,由此结合三角函数的诱导公式即可算出φ的值.解答:解:函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移
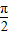 个单位后,得平移后的图象的函数解析式为
个单位后,得平移后的图象的函数解析式为y=cos[2(x-
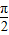 )+φ]=cos(2x+φ-π),
)+φ]=cos(2x+φ-π),而函数y=sin(2x+
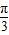 )=
)=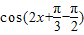 ,
,由函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移
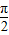 个单位后,与函数y=sin(2x+
个单位后,与函数y=sin(2x+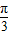 )的图象重合,得
)的图象重合,得2x+φ-π=
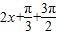 ,解得:x=
,解得:x=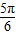 .
.符合-π≤φ<π.
故答案为
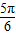 .
.点评:本题给出函数y=cos(2x+φ)的图象平移,求参数φ的值.着重考查了函数图象平移的公式、三角函数的诱导公式和函数y=Asin(ωx+φ)的图象变换等知识,属于基础题.

练习册系列答案
相关题目