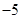题目内容
函数  的值域为
的值域为
A. | B. | C. | D. |
C
解析试题分析:因为 ,那么可知
,那么可知 ,而函数y=2x在R上递增函数,故有
,而函数y=2x在R上递增函数,故有 ,故选C.
,故选C.
考点:本试题主要考查了指数函数的值域的求解运用。
点评:解决该试题的关键是利用自变量的取值范围,得到幂指数的范围,结合指数函数y=2x的单调性来得到值域。

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
函数f (x)=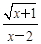 的定义域为
的定义域为
| A.[-1,2)∪(2,+∞) | B.(-∞,+∞) |
| C.[-1,+∞) | D.(-∞,2)∪(2,+∞) |
设f(x)是R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=
| A.3 | B.1 | C.-1 | D.-3 |
函数 的值域是 ( )
的值域是 ( )
A.(- ) ) | B.(-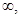 0) 0)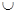 (0,+ (0,+ ) ) |
C.(-1,+ ) ) | D.(- ,-1) ,-1)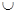 (0,+ (0,+ ) ) |
已知函数 是偶函数,当
是偶函数,当 时,
时, 恒成立,设
恒成立,设 ,则
,则 的大小关系为( )
的大小关系为( )
A. | B.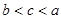 | C. | D. |
下列函数 中,满足对任意
中,满足对任意 ,
,
 (0,
(0, )且
)且 ,都有
,都有 的是 ( )
的是 ( )
A. = = | B. = = | C. = = | D. |
 是定义在[-6,6]上的偶函数,且
是定义在[-6,6]上的偶函数,且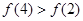 ,则下列各式一定成立的是( )
,则下列各式一定成立的是( )
A.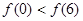 | B.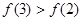 |
C.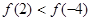 | D.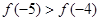 |
下列各图像中,不可能是函数 的图像的有几个( )
的图像的有几个( )
| A.1个 | B.2个 | C.3个 | D.4个 |
 ,定义运算
,定义运算 ,其中
,其中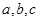 是常数,等式右边的运算是通常的加法和乘法运算。已知
是常数,等式右边的运算是通常的加法和乘法运算。已知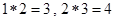 ,并且有一个非零常数
,并且有一个非零常数 ,使得对任意实数
,使得对任意实数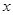 , 都有
, 都有 ,则
,则