Question

已知α为锐角，试证：1＜sinα+cosα≤．

Answer 1

思路解析：本例中，应在角α的终边上任取一点，应用三角函数的定义来解之．运用三角函数的定义，从而将三角问题转化为代数问题而获解，这是一种十分重要的解题方法，应引起重视．

证明：在角α的终边上任取一点P(x,y)(异于原点)，则sinα=,cosα=.

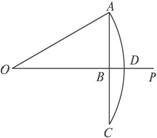
∵α为锐角，

∴x＞0,y＞0.

sinα+cosα=≤,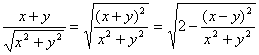

又sinα+cosα=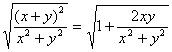＞1,

故1＜sinα+cosα≤.