题目内容
（本小题满分12分）已知等比数列
的公比
，
，
，等差数列
中
，
，其中
．
（1）求数列
，
的通项公式；
（2）设数列
，求数列
的前
项和
．
（1）
，
，.（2）
.
【解析】
试题分析：（1）由等比数列
的公比
,
，
，建立
方程组
,解得
，写出
的通项公式.
由已知，建立
（公差）的方程组，求得
，写出
的通项公式.
（2）由（1）知数列是以1为首项，2为公比的等比数列，数列
是以2为首项，2为公差的等差数列．应用“分组求和法”计算得到.
试题解析：（1）已知等比数列的公比,，
3分
等差数列中
设公差为
6分
（2）由（1）知数列是以1为首项，2为公比的等比数列，数列是以2为首项，2为公差的等差数列．
8分
12分
考点：1.等差数列；2.等比数列.
考点分析： 考点1：等比数列 试题属性- 题型：
- 难度：
- 考核：
- 年级：
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
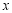（m），三块种植植物的矩形区域的总面积为
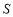（m2）．
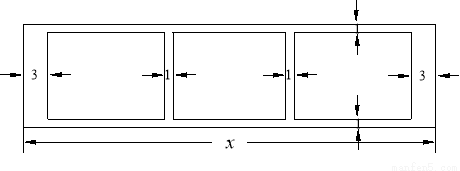
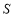关于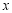
的函数关系式；
的最大值．
.
的解集；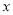
的不等式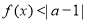
的解集非空，求实数
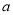的取值范围.
，
”的否定是“
，
，
，若
，则
或
”的逆否命题是真命题
在
上恒成立”
“
在
，则函数
只有一个零点”的逆命题为真命题
，
是函数
的两个极值点，且
，
且
．
时，求
的单调递减区间；
为定值；
的取值范围．
（
，
）的一个焦点
作一条渐近线的垂线，若垂足恰在线段
（
为坐标原点）的垂直平分线上，则双曲线的离心率为（ ）
B．
C．
D．
，则输出的
为（ ）
B．
D．
服从正态分布
，
，则
．
中，
是
边上一点，
，则
的长为 