Question

已知向量

a

=(2，2)，

b

=(x，y)．
（Ⅰ）若x，y∈{-1，0，1，2}，求向量

a

∥

b

的概率；
（Ⅱ）若x，y∈[-1，2]且均匀分布，求向量

a

，

b

的夹角是钝角的概率．

Answer 1

分析：（Ⅰ）先求出基本事件的个数，利用向量平行确定满足

a

∥

b

的事件个数，然后求概率；
（Ⅱ）求出向量

a

，

b

的夹角是钝角是等价条件，利用几何概型的概率公式求概率．

解答：解：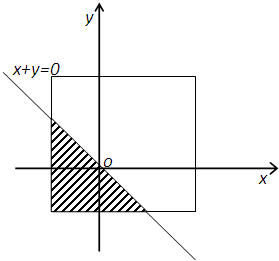
（Ⅰ）若x，y∈{-1，0，1，2}，则基本事件包括（-1，-1）、（-1，0）、（-1，1）、（-1，2）、
（0，-1）、（0，0）、（0，1）、（0，2）、（1，-1）、（1，0）、（1，1）、（1，2）、（2，-1）、（2，0）、（2，1）、（2，2），共计16个基本事件．
因为设向量

a

∥

b

的事件为A，若

a

∥

b

，则有2x-2y=0，即x=y，
则符合

a

∥

b

的

b

坐标为（-1，-1）、（0，0）、（1，1）、（2，2）共4个基本事件．
所以P(A)=

4

16

=

1

4

．
则向量

a

∥

b

的概率为

1

4

．
（Ⅱ）x，y∈[-1，2]且均匀分布，则基本事件表示为{（x，y）|-1≤x≤2，-1≤y≤2，x，y∈R}，
若设向量

a

，

b

的夹角是钝角的事件为B，
则应坐标

a

，

b

应满足

a

•

b

＜0且

a

，

b

不能共线反向，即

2x+2y＜0 x≠y

．
如图所示P（B）=

阴影部分面积

正方形面积

=

2×2× 1 2

3×3

=

2

9

．
所以向量

a

，

b

的夹角是钝角的概率为

2

9

…（12分）

点评：本题主要考查古典概型和几何概型概率的求法，利用列举法是解决古典概型的基本方法，利用数形结合是解决几何概型的基本方法．