题目内容
已知递增等差数列 中,
中,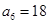 且
且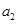 是
是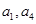 的等比中项,则它的第4项到第11项的和为
的等比中项,则它的第4项到第11项的和为
| A.180 | B.198 | C.189 | D.168 |
A
解析试题分析:设首项、公差分别为 ,则
,则 。因
。因 ,解得:
,解得: ,故所求的和为
,故所求的和为 。选A。
。选A。
考点:本题主要考查等差数列的通项公式和前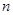 项和公式。
项和公式。
点评:数列中的基本问题,往往要依据题意建立关于基本量的方程(组)。灵活运用数列的性质,往往能简化解题过程。

练习册系列答案
相关题目
古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )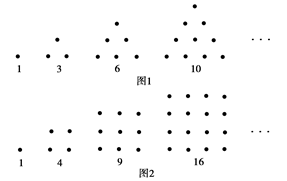
| A.289 | B.1024 | C.1225 | D.1378 |
在等差数列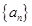 中a3+a4+a5=12,
中a3+a4+a5=12,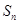 为数列
为数列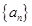 的前
的前 项和,则S7=( )
项和,则S7=( )
| A.14 | B.21 | C.28 | D.35 |
设 是等差数列
是等差数列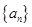 的前
的前 项和,已知
项和,已知 ,
,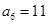 ,则
,则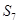 等于
等于
| A.13 | B.35 | C.49 | D.63 |
已知等差数列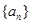 ,
, 则它的公差是( )
则它的公差是( )
| A.1 | B.2 | C.3 | D.4 |
在等差数列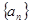 中,前四项之和为40,最后四项之和为80,所有项之和是210,则项数
中,前四项之和为40,最后四项之和为80,所有项之和是210,则项数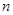 为( )
为( )
| A.12 | B.14 | C.15 | D.16 |
设 是等差数列,若
是等差数列,若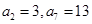 ,则数列
,则数列 前8项的和为( )
前8项的和为( )
| A.128 | B.80 | C.64 | D.56 |
在等差数列 中,
中, ,
, 表示数列
表示数列 的前
的前 项和,则
项和,则 ( )
( )
A. | B. | C. | D. |
设等差数列 的前
的前 项和为
项和为 ,已知
,已知 ,
, 则下列结论中正确的是( )
则下列结论中正确的是( )
A. | B. |
C. | D. |