题目内容
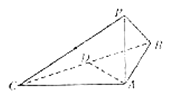
【题目】如图所示,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由余弦定理求出BC,因为![]() 为
为![]() 的中点,得BD=CD,因为
的中点,得BD=CD,因为![]() ,平方求出AD,利用勾股定理得AB⊥AD,结合PA⊥AD,得AD⊥平面PAB,从而AD⊥PB得证.
,平方求出AD,利用勾股定理得AB⊥AD,结合PA⊥AD,得AD⊥平面PAB,从而AD⊥PB得证.
(2)分别以直线AB,AD,AP为x轴,y轴,z轴建立空间直角坐标系,设PA=a,求出平面PBC的法向量,平面PAB的法向量,利用向量法求出a,然后求解VP﹣ABC=![]() ×S△ABC×PA即可.
×S△ABC×PA即可.
(1)在![]() 中,由余弦定理得
中,由余弦定理得![]() ,则
,则![]() .
.
因为![]() 为
为![]() 的中点,则
的中点,则![]() .
.
因为![]() ,则
,则![]()
![]() ,所以
,所以![]() .
.
因为![]() ,则
,则![]() .
.
因为![]() 底面
底面![]() ,则
,则![]() ,所以
,所以![]() 平面
平面![]() ,从而
,从而![]() .
.
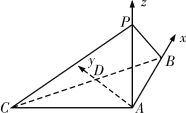
(2)分别以直线![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,如图所示.
轴建立空间直角坐标系,如图所示.
设![]() ,则点
,则点![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即![]() ,
,
取![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() 为平面
为平面![]() 的法向量,
的法向量,
则![]() ,即
,即![]() .
.
所以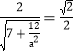 ,解得
,解得![]() ,所以
,所以![]() .
.
所以![]() .
.

【题目】郑州一中社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图:将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“围棋迷”与性别有关?

非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望
附:![]() ,
,
| 0.05 | 0.01 |
| 3.841 | 6.635 |
【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式
 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式:
 ,
,![]() )
)



