题目内容
已知双曲线 的渐近线方程为
的渐近线方程为 ,左焦点为F,过A(a,0),B(0,-b)的直线为l,原点到直线l的距离是
,左焦点为F,过A(a,0),B(0,-b)的直线为l,原点到直线l的距离是 .
.(1)求双曲线的方程;
(2)已知直线y=x+m交双曲线于不同的两点C,D,问是否存在实数m,使得以CD为直径的圆经过双曲线的左焦点F.若存在,求出m的值;若不存在,请说明理由.
【答案】分析:(1)根据双曲线的渐近线方程及原点到直线l的距离是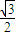 ,即可求双曲线的标准方程;
,即可求双曲线的标准方程;
(2)以CD为直径的圆经过双曲线的左焦点F,可知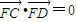 .将直线方程与双曲线方程联立,可得一元二次方程,利用韦达定理可将向量关系转化为坐标关系,从而得解.
.将直线方程与双曲线方程联立,可得一元二次方程,利用韦达定理可将向量关系转化为坐标关系,从而得解.
解答:解:(1)∵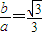 ,(2分)
,(2分)
原点到直线AB: 的距离,
的距离,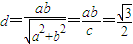 .(4分)
.(4分)
∴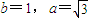 .故所求双曲线方程为
.故所求双曲线方程为 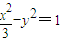 .(6分)
.(6分)
(2)把y=x+m代入x2-3y2=3中消去y,整理得 2x2+6mx+3m2+3=0.(8分)
设C(x1,y1),D(x2,y2),则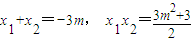 ,F(-2,0),
,F(-2,0),
因为以CD为直径的圆经过双曲线的左焦点F,所以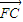
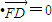 ,(10分)
,(10分)
可得 (x1+2)(x2+2)+y1y2=0把y1=x1+m,y1=x1+m代入,
解得: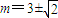 (13分)
(13分)
解△>0,得m2>2,
∴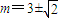 满足△>0,
满足△>0,
∴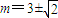 (14分)
(14分)
点评:本题的考点是直线与圆锥曲线的综合问题,主要考查双曲线的标准方程求解,考查直线与双曲线的位置关系,应注意判别式的验证.
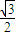 ,即可求双曲线的标准方程;
,即可求双曲线的标准方程;(2)以CD为直径的圆经过双曲线的左焦点F,可知
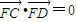 .将直线方程与双曲线方程联立,可得一元二次方程,利用韦达定理可将向量关系转化为坐标关系,从而得解.
.将直线方程与双曲线方程联立,可得一元二次方程,利用韦达定理可将向量关系转化为坐标关系,从而得解.解答:解:(1)∵
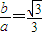 ,(2分)
,(2分)原点到直线AB:
 的距离,
的距离,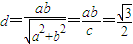 .(4分)
.(4分)∴
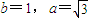 .故所求双曲线方程为
.故所求双曲线方程为 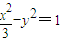 .(6分)
.(6分)(2)把y=x+m代入x2-3y2=3中消去y,整理得 2x2+6mx+3m2+3=0.(8分)
设C(x1,y1),D(x2,y2),则
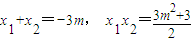 ,F(-2,0),
,F(-2,0),因为以CD为直径的圆经过双曲线的左焦点F,所以
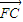
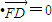 ,(10分)
,(10分)可得 (x1+2)(x2+2)+y1y2=0把y1=x1+m,y1=x1+m代入,
解得:
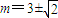 (13分)
(13分)解△>0,得m2>2,
∴
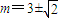 满足△>0,
满足△>0,∴
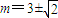 (14分)
(14分)点评:本题的考点是直线与圆锥曲线的综合问题,主要考查双曲线的标准方程求解,考查直线与双曲线的位置关系,应注意判别式的验证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线的渐近线方程为2x±3y=0,F(0,-5)为双曲线的一个焦点,则双曲线的方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|