题目内容
求圆x2+y2=1的切线方程,使此切线夹在两坐标轴正半轴间的线段最短.
解:设切点为(x1,y1),则切线方程为x1x+y1y=1,又因为x12+y12=1.
故切线与两坐标轴的交点为A(![]() ,0)、B(0,
,0)、B(0,![]() ).
).
因为x1>0,y1>0,所以|AB|=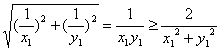 =2.
=2.
当且仅当x1=y1时,等号成立.代入x12+y12=1,可得x1=y1=![]() .
.
所以所求切线方程为x+y-![]() =0.
=0.

练习册系列答案
相关题目
题目内容
求圆x2+y2=1的切线方程,使此切线夹在两坐标轴正半轴间的线段最短.
解:设切点为(x1,y1),则切线方程为x1x+y1y=1,又因为x12+y12=1.
故切线与两坐标轴的交点为A(![]() ,0)、B(0,
,0)、B(0,![]() ).
).
因为x1>0,y1>0,所以|AB|=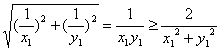 =2.
=2.
当且仅当x1=y1时,等号成立.代入x12+y12=1,可得x1=y1=![]() .
.
所以所求切线方程为x+y-![]() =0.
=0.
