题目内容
如图,设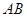 、
、 分别是圆
分别是圆 和椭圆
和椭圆 的弦,且弦的端点在
的弦,且弦的端点在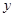 轴的异侧,端点
轴的异侧,端点 与
与 、
、 与
与 的横坐标分别相等,纵坐标分别同号.
的横坐标分别相等,纵坐标分别同号.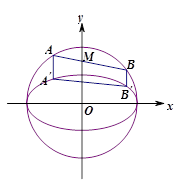
(Ⅰ)若弦 所在直线斜率为
所在直线斜率为 ,且弦
,且弦 的中点的横坐标为
的中点的横坐标为 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)若弦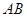 过定点
过定点 ,试探究弦
,试探究弦 是否也必过某个定点. 若有,请证明;若没有,请说明理由.
是否也必过某个定点. 若有,请证明;若没有,请说明理由.
(Ⅰ)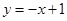 ;(Ⅱ)弦
;(Ⅱ)弦 必过定点
必过定点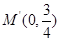 .
.
解析试题分析:(Ⅰ)由题意得:直线 的方程为
的方程为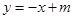
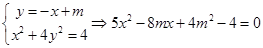 ,
,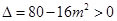 ,
, 设
设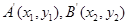
 ,将
,将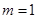 代入
代入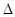 检验符合题意,
检验符合题意,
故满足题意的直线 方程为:
方程为: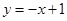
(Ⅱ)解法一:由(Ⅰ)得:圆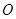 的方程为:
的方程为: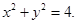 分
分
设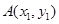 、
、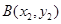 、
、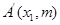 、
、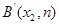 ,
,
∵点 在圆
在圆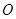 上, ∴
上, ∴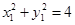 ,………①
,………①
∵点 在椭圆
在椭圆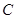 上, ∴
上, ∴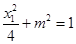 ,………②
,………②
联立方程①②解得: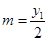 ,同理解得:
,同理解得: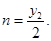
∴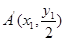 、
、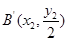 ∵弦
∵弦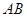 过定点
过定点 ,
,
∴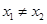 且
且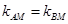 ,即
,即 ,
,
化简得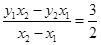
直线 的方程为:
的方程为: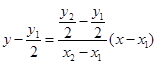 ,即
,即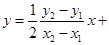
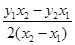 ,
,
由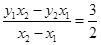 得直线
得直线 的方程为:
的方程为: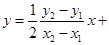
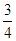 ,
,
∴弦 必过定点
必过定点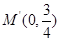 .
.
解法二:由(Ⅰ)得:圆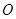 的方程为:
的方程为:
设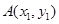 、
、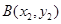 ,
,
∵圆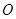 上的每一点横坐标不变,纵坐标缩短为原来的
上的每一点横坐标不变,纵坐标缩短为原来的 倍可得到椭圆
倍可得到椭圆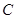 ,
,
又端点 与
与 、
、 与
与 的横坐标分别相等,纵坐标分别同号,
的横坐标分别相等,纵坐标分别同号,
∴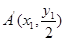 、
、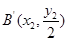
由弦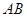 过定点
过定点 ,猜想弦
,猜想弦 过定点
过定点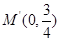 .
.
∵弦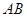 过定点
过定点 ,∴
,∴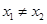 且
且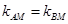 ,即
,即 ……①
……① 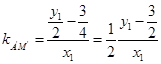 ,
,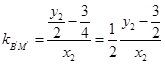 ,
,
由①得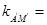
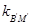 ,
,
∴弦 必过定点
必过定点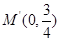 .
.
考点:本题主要考查直线、圆、椭圆等基础知识的综合应用。
点评:本题以直线、圆、椭圆为载体,综合考查推理论证能力、数形结合思想、化归与转化思想、函数与方程思想.

练习册系列答案
相关题目
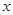 轴对称,它的顶点在坐标原点,并且经过点
轴对称,它的顶点在坐标原点,并且经过点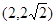
 过抛物线的焦点F,与抛物线交于A、B两点,线段AB的中点M的横坐标为3,求弦长
过抛物线的焦点F,与抛物线交于A、B两点,线段AB的中点M的横坐标为3,求弦长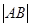 以及直线
以及直线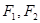 分别为椭圆
分别为椭圆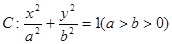 的左、右焦点,点
的左、右焦点,点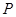 为椭圆上任意一点,
为椭圆上任意一点,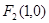 的距离的最大值为
的距离的最大值为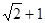 .
.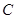 的方程。
的方程。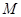 的坐标为
的坐标为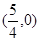 ,过点
,过点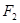 且斜率为
且斜率为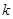 的直线
的直线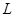 与椭圆
与椭圆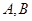 两点。对于任意的
两点。对于任意的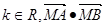 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。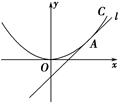
 :
: 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为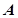 ,过点
,过点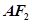 垂直的直线交
垂直的直线交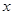 轴负半轴于点
轴负半轴于点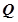 ,且
,且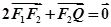 .
.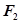 三点的圆恰好与直线
三点的圆恰好与直线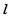 :
: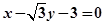 相切,
相切, ,长轴长为
,长轴长为 ,离心率
,离心率 ,过右焦点
,过右焦点 的直线
的直线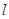 交
交 ,
, 两点:
两点: 的面积;
的面积;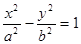 的离心率
的离心率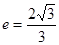 ,过
,过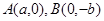 的直线到原点的距离是
的直线到原点的距离是
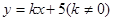 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.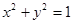 过椭圆
过椭圆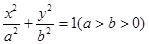 的两焦点,与椭圆有且仅有两个
的两焦点,与椭圆有且仅有两个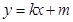 与圆
与圆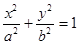 相交于
相交于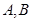 两点记
两点记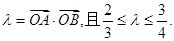
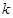 的取值范围;
的取值范围;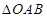 的面积S的取值范围.
的面积S的取值范围. 轴的负半轴上,过点
轴的负半轴上,过点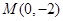 作直线
作直线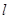 与抛物线交于A,B两点,且满足
与抛物线交于A,B两点,且满足 ,
,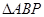 面积的的最大值.
面积的的最大值.