题目内容
已知 ,则导函数
,则导函数 是( )
是( )
| A.仅有最小值的奇函数 | B.既有最大值,又有最小值的偶函数 |
| C.仅有最大值的偶函数 | D.既有最大值,又有最小值的奇函数 |
D
解析试题分析:因为 ,依题意可知该函数的定义域为
,依题意可知该函数的定义域为 ,关于原点对称,且
,关于原点对称,且 ,所以函数
,所以函数 为奇函数,另一方面
为奇函数,另一方面 ,因为
,因为 ,所以
,所以 ,所以
,所以 ,故
,故 在
在 单调递增,最大值为
单调递增,最大值为 ,最小值为
,最小值为 ,综上可知选D.
,综上可知选D.
考点:1.函数的单调性与极值;2.函数的奇偶性.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
已知点 ,
, 在第二象限,则
在第二象限,则 的一个变化区间是
的一个变化区间是
A. | B. | C. | D. |
若 是定义在R上的连续函数,且
是定义在R上的连续函数,且 ,则
,则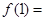 ( )
( )
| A.2 | B.1 | C.0 | D.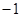 |
 =" " ( )
=" " ( )
| A.—6 | B.0 | C.6 | D.3 |
设函数f(x)=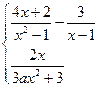
 在点x=1处连续,则a等于
在点x=1处连续,则a等于
A.-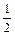 | B.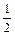 | C.-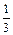 | D.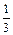 |
已知映射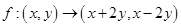 ,在映射
,在映射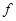 下
下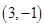 的原象是( )
的原象是( )
A.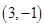 | B.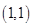 | C.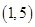 | D.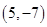 |
 在(0,1)内是增函数.
在(0,1)内是增函数. 的取值范围;
的取值范围; ,求证:
,求证: .
.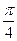 .
. ?若存在,求出最小的正整数k,否则请说明理由.
?若存在,求出最小的正整数k,否则请说明理由. 数
数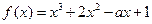 .
. 在点
在点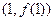 处的切线斜率为4,求实
处的切线斜率为4,求实 数
数 的值;
的值;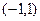 上是单调函数,求实数
上是单调函数,求实数