题目内容
在圆x2+y2-5y=0内,过点 作n条弦(n∈N+),它们的长构成等差数列{an},若a1为过该点最短的弦,an为过该点最长的弦,且公差
作n条弦(n∈N+),它们的长构成等差数列{an},若a1为过该点最短的弦,an为过该点最长的弦,且公差 ,则n的值为
,则n的值为
- A.4
- B.5
- C.6
- D.7
B
分析:根据题设条件求出a1和an,然后由公差 ,可以推导出n的值.
,可以推导出n的值.
解答:由题意知a1对应的方程是 ,an对应的方程的方程为
,an对应的方程的方程为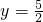 ,
,
把 代入圆x2+y2-5y=0得到交点坐标为
代入圆x2+y2-5y=0得到交点坐标为 和
和 ,
,
∴a1=4,an=5,
∴4+(n-1)d=5,∴ .
.
∵公差 ,∴
,∴ ,
,
解得4<n<6.故选B.
点评:本题考查圆的方程和数列的知识,解题时要注意公式的灵活运用.
分析:根据题设条件求出a1和an,然后由公差
 ,可以推导出n的值.
,可以推导出n的值.解答:由题意知a1对应的方程是
 ,an对应的方程的方程为
,an对应的方程的方程为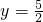 ,
,把
 代入圆x2+y2-5y=0得到交点坐标为
代入圆x2+y2-5y=0得到交点坐标为 和
和 ,
,∴a1=4,an=5,
∴4+(n-1)d=5,∴
 .
.∵公差
 ,∴
,∴ ,
,解得4<n<6.故选B.
点评:本题考查圆的方程和数列的知识,解题时要注意公式的灵活运用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 作n条弦(n∈N+),它们的长构成等差数列{an},若a1为过该点最短的弦,an为过该点最长的弦,且公差
作n条弦(n∈N+),它们的长构成等差数列{an},若a1为过该点最短的弦,an为过该点最长的弦,且公差 ,则n的值为( )
,则n的值为( )