题目内容
已知函数f(x)满足:①定义域为R;②对任意x∈R,有f(x+2)=2f(x);③当x∈[-1,1]时,f(x)=-|x|+1.记g(x)=f(x)-log4|x|,根据以上信息,可以得到函数g(x)在区间[-10,10]内的零点个数是 .
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:由g(x)=f(x)-log4|x|=0,得f(x)=log4|x|,在同一坐标系中画出函数f(x)与函数y=log4|x|的图象,利用图象的交点情况即可得到结论.
解答:
解:由g(x)=f(x)-log4|x|=0,得f(x)=log4|x|,在同一坐标系中画出函数f(x)与函数y=log4|x|的图象:
观察图象可得:两个函数的图象共有11个交点
则方程f(x)=log4|x|在区间[-10,10]内的解的个数是:11.
即函数g(x)在区间[-10,10]内的零点个数是11.
故答案为:11.

观察图象可得:两个函数的图象共有11个交点
则方程f(x)=log4|x|在区间[-10,10]内的解的个数是:11.
即函数g(x)在区间[-10,10]内的零点个数是11.
故答案为:11.
点评:本小题主要考查根的存在性及根的个数判断、函数图象的应用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
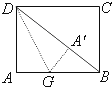 如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为
如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为