题目内容
11.已知α为第二象限的角,sinα=$\frac{3}{5}$,则$tan\frac{α}{2}$=3,tan2α=$-\frac{24}{7}$.分析 先由已知求得$\frac{α}{2}$的范围,求出tanα的值,再由正切函数的二倍角公式可得答案.
解答 解:∵α为第二象限的角,
∴可得:$\frac{α}{2}$∈(kπ$+\frac{π}{4}$,k$π+\frac{π}{2}$),k∈Z,
∴tan$\frac{α}{2}$>0,
又∵sinα=$\frac{3}{5}$,∴cosα=-$\frac{4}{5}$,tanα=$\frac{sinα}{cosα}$=-$\frac{3}{4}$,
∴tanα=-$\frac{3}{4}$=$\frac{2tan\frac{α}{2}}{1-ta{n}^{2}\frac{α}{2}}$,整理可得:3tan2$\frac{α}{2}$-8tan$\frac{α}{2}$-3=0,解得:tan$\frac{α}{2}$=3或-$\frac{1}{3}$(舍去).
tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$-\frac{24}{7}$.
故答案为:3,$-\frac{24}{7}$.
点评 本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
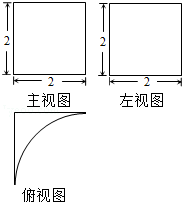 某几何体的三视图如图所示,其中俯视图为半径为2的四分之一个圆弧,则该几何体的体积为8-2π,表面积为16.
某几何体的三视图如图所示,其中俯视图为半径为2的四分之一个圆弧,则该几何体的体积为8-2π,表面积为16.