题目内容
已知
=3，求
.
解：由=3，可设ax2+bx+1=（x－1）（ax+c）.
∴ax2+bx+1=ax2+（c－a）x－c且
（ax+c）=3.
∴
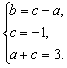
解得c=－1，a=4，b=－5.
∴
= 
=－5.
点评：函数f（x）=
在x=1附近有意义，且ax2+bx+1中含有因式x－1是解决本题的关键.
练习册系列答案
相关题目
=3，求.题目内容
已知=3，求.
解：由=3，可设ax2+bx+1=（x－1）（ax+c）.
∴ax2+bx+1=ax2+（c－a）x－c且
（ax+c）=3.
∴
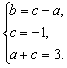
解得c=－1，a=4，b=－5.
∴= =－5.
点评：函数f（x）=在x=1附近有意义，且ax2+bx+1中含有因式x－1是解决本题的关键.
+
=3，求a2+a-2的值.
+
=3，求下列各式的值.
.
=3，求
的值.
=3，
+
=3，求a+a-1及a2+a-2的值；