题目内容
化简求值:(1)已知
 +
+ =3,求a+a-1及a2+a-2的值;
=3,求a+a-1及a2+a-2的值;(2)(lg5)2+lg2×lg50.
【答案】分析:(1)由 +
+ =3,两边平方,得a+a-1+2=9,故a+a-1=7.把a+a-1=7两边平方,得a2+a-2+2=49,由此能求出a2+a-2.
=3,两边平方,得a+a-1+2=9,故a+a-1=7.把a+a-1=7两边平方,得a2+a-2+2=49,由此能求出a2+a-2.
(2)由对数的运算性质,把(lg5)2+lg2×lg50等价转化为(lg5)2+lg2×(lg5+1),进一步简化为lg5(lg5+lg2)+lg2,由此能求出结果.
解答:解:(1)∵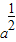 +
+ =3,
=3,
∴两边平方,得a+a-1+2=9,
∴a+a-1=7.
把a+a-1=7两边平方,得a2+a-2+2=49,
∴a2+a-2=47.
(2)(lg5)2+lg2×lg50
=(lg5)2+lg2×(lg5+1)
=(lg5)2+lg2lg5+lg2
=lg5(lg5+lg2)+lg2
=lg5+lg2
=1.
点评:第(1)题考查指数式的性质和运算法则,第(2)题考查对数的性质和运算法则,是基础题.解题时要认真审题,仔细解答.
 +
+ =3,两边平方,得a+a-1+2=9,故a+a-1=7.把a+a-1=7两边平方,得a2+a-2+2=49,由此能求出a2+a-2.
=3,两边平方,得a+a-1+2=9,故a+a-1=7.把a+a-1=7两边平方,得a2+a-2+2=49,由此能求出a2+a-2.(2)由对数的运算性质,把(lg5)2+lg2×lg50等价转化为(lg5)2+lg2×(lg5+1),进一步简化为lg5(lg5+lg2)+lg2,由此能求出结果.
解答:解:(1)∵
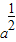 +
+ =3,
=3,∴两边平方,得a+a-1+2=9,
∴a+a-1=7.
把a+a-1=7两边平方,得a2+a-2+2=49,
∴a2+a-2=47.
(2)(lg5)2+lg2×lg50
=(lg5)2+lg2×(lg5+1)
=(lg5)2+lg2lg5+lg2
=lg5(lg5+lg2)+lg2
=lg5+lg2
=1.
点评:第(1)题考查指数式的性质和运算法则,第(2)题考查对数的性质和运算法则,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 =3,求a+a-1;
=3,求a+a-1;