题目内容
若函数在y=ax2+bx-c(-∞,0]是单调函数,则y=2ax+b的图象不可能是( )A.

B.

C.

D.

【答案】分析:利用函数y=ax2+bx-c(-∞,0]是单调函数,得到a,b的关系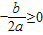 ,利用a,b的取值关系判断直线y=2ax+b的图象即可.
,利用a,b的取值关系判断直线y=2ax+b的图象即可.
解答:解:若函数y=ax2+bx-c为二次函数,则a≠0,二次函数的对称轴为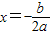 ,要使在y=ax2+bx-c(-∞,0]是单调函数,则
,要使在y=ax2+bx-c(-∞,0]是单调函数,则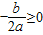 .
.
若a=0,则要使y=bx-c(-∞,0]是单调函数,则b≠0.
A中a=0,b<0,显然满足条件.
B中,b>0,2a>0,不满足条件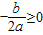 .
.
C中,2a>0,b<0,满足条件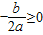 .
.
D中,2a<0,b=0,满足条件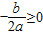 .
.
所以只有B不可能.
故选B.
点评:本题主要考查函数图象的识别和判断,利用函数的单调性确定a,b的取值关系,是解决本题的关键,要注意对a进行分类讨论.
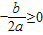 ,利用a,b的取值关系判断直线y=2ax+b的图象即可.
,利用a,b的取值关系判断直线y=2ax+b的图象即可.解答:解:若函数y=ax2+bx-c为二次函数,则a≠0,二次函数的对称轴为
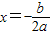 ,要使在y=ax2+bx-c(-∞,0]是单调函数,则
,要使在y=ax2+bx-c(-∞,0]是单调函数,则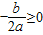 .
.若a=0,则要使y=bx-c(-∞,0]是单调函数,则b≠0.
A中a=0,b<0,显然满足条件.
B中,b>0,2a>0,不满足条件
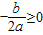 .
.C中,2a>0,b<0,满足条件
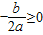 .
.D中,2a<0,b=0,满足条件
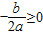 .
.所以只有B不可能.
故选B.
点评:本题主要考查函数图象的识别和判断,利用函数的单调性确定a,b的取值关系,是解决本题的关键,要注意对a进行分类讨论.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目