Question

已知向量

OP

=(x，y)，当实数x，y满足约束条件：

y≤0 y≥x 2x+y+k≥0

（k为常数）时，能使|

OP

|max=5的k值为

10

．

Answer 1

分析：作出题中不等式组表示的平面区域，得到如图所示的△OAB及其内部，根据向量模的公式算出

|OA|

=|

k

2

|，

|OB|

=

2

3

|k|，可得

|OA|

＞

|OB|

．运动区域内的点P，当P与点A重合时|

OP

| 达到最大值，由此建立关于k的等式，解之即可得到满足条件的k值．

解答：解：根据题意，作出不等式组

y≤0 y≥x 2x+y+k≥0

所表示的平面区域，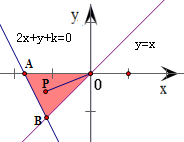
得到如图所示的△OAB及其内部，其中A（-

k

2

，0），B（-

k

3

，-

k

3

）
∵

|OA|

=

(- k 2 )2+02

=|

k

2

|，

|OB|

=

(- k 3 )2+(- k 3 )2

=

2

3

|k|，（k≠0）
∴

|OA|

＞

|OB|

，点P（x，y）为区域内部一个动点，运动点P可得当P与点A重合时，|

OP

| 达到最大值，
因此，若|

OP

|max=5，则|

OP

| =

|OA|

=|

k

2

|=5，解之得k=±10．
∵△OAB在第三象限，可得k＞0，∴k=10
故答案为：10

点评：本题给出二元一次不等式组，求满足条件“|

OP

|max=5”的k值．着重考查了向量模的公式、二元一次不等式组表示的平面区域和简单的线性规划等知识，属于中档题．