题目内容
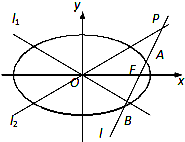 如图,已知椭圆C的方程为
如图,已知椭圆C的方程为| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)若l1与l2的夹角为60°,且双曲线的焦距为4,求椭圆C的方程;
(Ⅱ)求
| |FA| |
| |AP| |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知得∠POF=30°,从而a=
b.由此能求出椭圆C的方程.
(Ⅱ)直线l的方程为y=
(x-c),直线l2的方程为y=
x,联立直线l与l2的方程,解得点P(
,
),由此入手结合已知条件能求出
的最大值.
| 3 |
(Ⅱ)直线l的方程为y=
| a |
| b |
| b |
| a |
| a2 |
| c |
| ab |
| c |
| |FA| |
| |AP| |
解答:
解:(Ⅰ)因为双曲线方程为
-
=1,
所以双曲线的渐近线方程为y=±
x.
因为两渐近线的夹角为60°且
<1,所以∠POF=30°.
所以
=tan30°=
. 所以a=
b.
因为c=2,所以a2+b2=4,所以a=
,b=1.
所以椭圆C的方程为
+y2=1.…(4分)
(Ⅱ)因为l⊥l1,所以直线l的方程为y=
(x-c),其中c=
.…(5分)
直线l2的方程为y=
x,联立直线l与l2的方程,解得点P(
,
).…(6分)
设
=λ,则
=λ
.…(7分)
因为点F(c,0),设点A(x0,y0),则有(x0-c,y0)=λ(
-x0,
-y0).
解得x0=
,y0=
.…(8分)
因为点A(x0,y0)在椭圆
+
=1上,
所以
+
=1.
即(c2+λa2)2+λ2a4=(1+λ)2a2c2.
等式两边同除以a4,得(e2+λ)2+λ2=e2(1+λ)2,e∈(0,1),
所以λ2=
=-(2-e2+
)+3≤-2
+3=3-2
=(
-1)2.…(10分)
所以当2-e2=
,即e=
时,λ取得最大值
-1.
故
的最大值为
-1.…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
所以双曲线的渐近线方程为y=±
| b |
| a |
因为两渐近线的夹角为60°且
| b |
| a |
所以
| b |
| a |
| ||
| 3 |
| 3 |
因为c=2,所以a2+b2=4,所以a=
| 3 |
所以椭圆C的方程为
| x2 |
| 3 |
(Ⅱ)因为l⊥l1,所以直线l的方程为y=
| a |
| b |
| a2-b2 |
直线l2的方程为y=
| b |
| a |
| a2 |
| c |
| ab |
| c |
设
| |FA| |
| |AP| |
| FA |
| AP |
因为点F(c,0),设点A(x0,y0),则有(x0-c,y0)=λ(
| a2 |
| c |
| ab |
| c |
解得x0=
| c2+λa2 |
| c(1+λ) |
| λab |
| c(1+λ) |
因为点A(x0,y0)在椭圆
| x2 |
| a2 |
| y2 |
| b2 |
所以
| (c2+λa2)2 |
| a2c2(1+λ)2 |
| (λab)2 |
| b2c2(1+λ)2 |
即(c2+λa2)2+λ2a4=(1+λ)2a2c2.
等式两边同除以a4,得(e2+λ)2+λ2=e2(1+λ)2,e∈(0,1),
所以λ2=
| e2-e4 |
| 2-e2 |
| 2 |
| 2-e2 |
(2-e)2•
|
| 2 |
| 2 |
所以当2-e2=
| 2 |
| 2-e2 |
2-
|
| 2 |
故
| |FA| |
| |AP| |
| 2 |
点评:本题考查椭圆方程的求法,考查两线段比值的最大值的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
△ABC中,A=
,BC=
,AC=
,则角B等于( )
| π |
| 3 |
| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中值域为R的函数有( )
①y=(
)x ②y=x2 ③y=
④y=log2x.
①y=(
| 1 |
| 2 |
| 1 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
设θ为两个非零向量
,
的夹角,已知对任意实数t,|
+t
|的最小值为1( )
| a |
| b |
| b |
| a |
A、若|
| ||
B、若|
| ||
C、若θ确定,则|
| ||
D、若θ确定,则|
|
如果变量x,y满足约束条件
,则
的取值范围是( )
|
| 2y-2x-2 |
| 2x+1 |
A、[
| ||||
B、(-∞,
| ||||
C、(-∞,
| ||||
D、[
|
已知a,b,c∈R,则“abc<0”是ax2+by2=c表示双曲线的 ( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
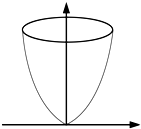 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是