题目内容
20.已知F1是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,点B的坐标为(0,b),直线F1B与双曲线C的两条渐近线分别交于P,Q两点,若$\overrightarrow{QP}$=4$\overrightarrow{P{F}_{1}}$,则双曲线C的离心率为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2 |
分析 求出P,Q的坐标,利用$\overrightarrow{QP}$=4$\overrightarrow{P{F}_{1}}$,求出双曲线C的离心率.
解答 解:由题意,kPQ=$\frac{b}{c}$.
∴直线PQ为:y=$\frac{b}{c}$(x+c),与y=$\frac{b}{a}$x.联立得:Q($\frac{ac}{c-a}$,$\frac{bc}{c-a}$);
与y=-$\frac{b}{a}$x.联立得:P(-$\frac{ac}{c+a}$,$\frac{bc}{c+a}$).
∵$\overrightarrow{QP}$=4$\overrightarrow{P{F}_{1}}$,
∴-$\frac{ac}{c+a}$-$\frac{ac}{c-a}$=4(-c+$\frac{ac}{c+a}$),
∴e=$\frac{c}{a}$=$\frac{3}{2}$.
故选:B.
点评 本题考查双曲线C的离心率,考查学生的计算能力,确定P,Q的坐标是关键.

练习册系列答案
相关题目
11.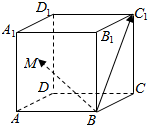 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点M是左侧面ADD1A1上的一个动点,满足$\overrightarrow{B{C}_{1}}$•$\overrightarrow{BM}$=1,则$\overrightarrow{B{C}_{1}}$与$\overrightarrow{BM}$的夹角的最大值为( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点M是左侧面ADD1A1上的一个动点,满足$\overrightarrow{B{C}_{1}}$•$\overrightarrow{BM}$=1,则$\overrightarrow{B{C}_{1}}$与$\overrightarrow{BM}$的夹角的最大值为( )
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点M是左侧面ADD1A1上的一个动点,满足$\overrightarrow{B{C}_{1}}$•$\overrightarrow{BM}$=1,则$\overrightarrow{B{C}_{1}}$与$\overrightarrow{BM}$的夹角的最大值为( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点M是左侧面ADD1A1上的一个动点,满足$\overrightarrow{B{C}_{1}}$•$\overrightarrow{BM}$=1,则$\overrightarrow{B{C}_{1}}$与$\overrightarrow{BM}$的夹角的最大值为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
15.a=log0.76,b=60.7,c=0.70.6,则a,b,c的大小关系为( )
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | b>c>a |
12.已知全集R,集合M={x|x>1},N={x||x|≤2},则(∁RM)∩N等于( )
| A. | (-2,1] | B. | [-2,1) | C. | [-2,1] | D. | [1,2] |
9.将函数y=cos(2x+$\frac{π}{3}$)的图象向左平移$\frac{π}{12}$单位后,得到的图象的函数解析式为( )
| A. | y=cos(2x+$\frac{5π}{12}$) | B. | y=-sin2x | C. | y=cos(2x+$\frac{π}{4}$) | D. | y=sin2x |