题目内容
求函数f(x)=
的最大值与最小值.
解:先求定义域0≤x≤1.设x=sin2t，t∈［0,
］,则1-x=cos2t.且sint ≥0,cost≥0.
∴f(x)=|sint|+|cost|=sint+cost=
(sint·
+cost·
)=
sin(t+
),
t+
∈［
,
π］,如图的正弦线，
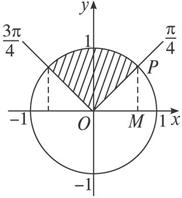
则sin(t+
)∈［
,1］，∴f(x)∈［1,
］，
即f(x)最大=
,f(x)最小=1.
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
的最大值与最小值.孟建平小学滚动测试系列答案
cos
)＋B(A＞0，ω＞0，
的最小值
的最小值．
，其中
．
与
能否平行，并说明理由？
＝(
，
)，
＝(2，cos2x)．
，试判断
，求函数f(x)＝
的最小值．