题目内容
在△ABC中,A:B=1:2,C的平分线CD把三角形面积分成3:2两部分,则cosA=______.
由题意可得,S△ACD:S△BCD=3:2,即
|CA|•|CD|sin
C:
|CB|•|CD|sin
C=3:2,
所以|CA|:|CB|=3:2,
由正弦定理得,
=
,即
=
,
所以
=
,所以cosA=
,
故答案为:
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以|CA|:|CB|=3:2,
由正弦定理得,
| sinB |
| sinA |
| 3 |
| 2 |
| sin2A |
| sinA |
| 3 |
| 2 |
所以
| 2sinAcosA |
| sinA |
| 3 |
| 2 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |

练习册系列答案
相关题目
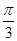 , a=
, a=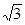 , b=1,则c= ( )
, b=1,则c= ( ) 9
9 中,若
中,若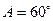 ,
, ,此三角形的面积
,此三角形的面积 ,则
,则 边的长为( )
边的长为( )



