题目内容
8.在直角坐标系xOy中,圆C1:(x+$\sqrt{3}$)2+y2=4,曲线C2的参数方程为$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),并以O为极点,x轴正半轴建立极坐标系.(1)写出圆C1的圆心C1的直角坐标,并将C2化为极坐标方程;
(2)若直线C3的极坐标方程为θ=$\frac{π}{3}$(ρ∈R),C2与C3相交于A,B两点,求△ABC1的面积(C1为圆C1的圆心.
分析 (1)圆C1:(x+$\sqrt{3}$)2+y2=4,可得圆心C1$(-\sqrt{3},0)$.曲线C2的参数方程为$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),利用平方关系消去参数θ可得普通方程,展开利用互化公式可得极坐标方程.
(2)直线C3的极坐标方程为θ=$\frac{π}{3}$(ρ∈R),可得直角坐标方程:y=$\sqrt{3}$x.原点O是C2与C3的一个交点,不妨设为A点,则|AB|,|AC1|,∠BAC1=120°,可得△ABC1的面积S=$\frac{1}{2}$|AB|•|AC1|sin120°.
解答 解:(1)圆C1:(x+$\sqrt{3}$)2+y2=4,可得圆心C1$(-\sqrt{3},0)$.
曲线C2的参数方程为$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),利用平方关系消去参数θ可得普通方程:(x-2)2+y2=4,
展开可得:x2+y2-4x=0,可得极坐标方程:ρ2-4ρcosθ=0,即ρ=4cosθ.
(2)直线C3的极坐标方程为θ=$\frac{π}{3}$(ρ∈R),可得直角坐标方程:y=$\sqrt{3}$x.原点O是C2与C3的一个交点,不妨设为A点,则|AB|=2×2cos60°=2,|AC1|=$\sqrt{3}$,∠BAC1=120°,
∴△ABC1的面积S=$\frac{1}{2}$|AB|•|AC1|sin120°=$\frac{1}{2}×2×\sqrt{3}×\frac{\sqrt{3}}{2}$=$\frac{3}{2}$.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、直线与圆的位置关系、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

| A. | 4 | B. | 3 | C. | 2 | D. | $\frac{3}{2}$ |

| A. | $\sqrt{5}$+15 | B. | 2$\sqrt{5}$+20 | C. | 15 | D. | 2$\sqrt{5}$+12 |

| A. | S=19+20;T=19×20 | B. | S=19×20;T=19+20 | ||
| C. | S=1×2×3×…×20; T=1+2+3+…+20 | D. | S=1+2+3+…+20; T=1×2×3×…×20 |
| A. | e2x | B. | e2x-1 | C. | e2x-2 | D. | e2x-4 |
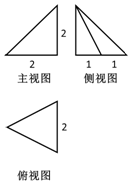
| A. | $\frac{4}{3}$ | B. | $7+\sqrt{5}$ | C. | $5+\sqrt{5}$ | D. | $7+2\sqrt{5}$ |

 2017年高考特别强调了要增加对数学文化的考查,为此瓦房店市高级中学高三年级数学组特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
2017年高考特别强调了要增加对数学文化的考查,为此瓦房店市高级中学高三年级数学组特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).