题目内容
已知函数f(x)=sin +2cos2x-1
+2cos2x-1
(Ⅰ)求函数f(x)的单调递增区间,并说明把 图像经过怎样的变换得到
图像经过怎样的变换得到 的图像。
的图像。
(Ⅱ)若在△ABC中,a、b、c分别是角A、B、C的对边,且a=1,b+c=2,f(A)= ,求△ABC的面积.
,求△ABC的面积.
解 (1)∵f(x)=sin +2cos2x-1=
+2cos2x-1= sin2x-
sin2x- cos2x+cos2x=
cos2x+cos2x= sin 2x+
sin 2x+ cos 2x=sin
cos 2x=sin .
.
∴函数f(x)的单调递增区间是 (k∈Z).
(k∈Z).
可将 图像横坐标向右平移
图像横坐标向右平移 个单位,纵坐标不变得到
个单位,纵坐标不变得到 的图像。
的图像。
(2)∵f(A)= , ∴sin
, ∴sin  =
= . 又0<A<π, ∴
. 又0<A<π, ∴ <2A+
<2A+ <
< .
.
∴2A+ =
= ,故A=
,故A= . 在△ABC中,∵a=1,b+c=2,A=
. 在△ABC中,∵a=1,b+c=2,A= ,
,
∴1=b2+c2-2bccos A,即1=4-3bc. ∴bc=1. ∴S△ABC= bcsin A=
bcsin A= .
.

练习册系列答案
相关题目
 的光线经
的光线经 轴上点
轴上点 反射后,经过不等式组
反射后,经过不等式组 所表示的区域,则
所表示的区域,则 的取值范围 ;
的取值范围 ;  时,求函数y=x+
时,求函数y=x+ 的最大值.
的最大值.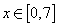 时,输出的y的取值范围是( )
时,输出的y的取值范围是( )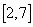 (B)
(B)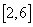 (C)
(C)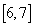 (D)
(D) 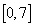
 :
: 的左右焦点分别为
的左右焦点分别为 ,双曲线
,双曲线 :
: 与椭圆
与椭圆 ,且三角形
,且三角形 的面积小于
的面积小于 ;②当
;②当 时,
时, ;③分别以
;③分别以 为直径作圆,这两个圆相内切; ④曲线
为直径作圆,这两个圆相内切; ④曲线
 为圆O的直径,C、D是圆O上的两个点,
为圆O的直径,C、D是圆O上的两个点, 于
于 ,
, 交
交 于
于 ,
, 于
于 ,
, .
. 

 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 ( )
( ) B.
B.  C.
C.  D.
D. 
 四点在同一圆上,
四点在同一圆上, 与
与 的延长线交于点
的延长线交于点 ,点
,点 在
在 的延长线上.
的延长线上. ,求
,求 的值;
的值; ,证明:
,证明: .
.
 ,则函数
,则函数 的零点个数为___________.
的零点个数为___________.