题目内容
已知函数![]() ,
,![]() ,
,![]() 图象与
图象与![]() 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为![]() ,
,![]() 与
与![]() 轴的交点N处的切线为
轴的交点N处的切线为![]() , 并且
, 并且![]() 与
与![]() 平行.
平行.
(1)求![]() 的值;
的值;
(2)已知实数t∈R,求![]() 的取值范围及函数
的取值范围及函数![]() 的最小值;
的最小值;
(3![]() )令
)令![]() ,
,![]() 给定
给定![]() ,对于两个大于1的正数
,对于两个大于1的正数![]() ,存在实数
,存在实数![]() 满足:
满足:![]() ,
,![]() ,并且使得不等式
,并且使得不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.

![]() ,
,![]()
![]()
所以![]() 在区间
在区间![]() 上单调递增
上单调递增
∴![]() 时,
时,![]()
①当![]() 时,有
时,有![]() ,
,
![]() ,
,
得![]() ,同理
,同理![]() ,
,
∴ 由![]() 的单调性知
的单调性知 ![]()
![]() 、
、![]()
从而有![]() ,符合题设.
,符合题设.
②当![]() 时,
时,![]() ,
,
![]() ,
,
由![]() 的单调性知
的单调性知 ![]()
![]() ,
,
∴![]() ,与题设不
,与题设不
③当![]() 时,同理可得
时,同理可得![]() ,
,
得![]() ,与题设不符.
,与题设不符.
∴综合①、②、③得![]()

练习册系列答案
相关题目
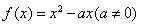
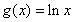
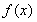
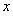
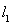
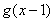
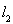
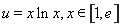
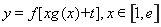
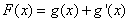
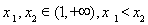
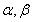
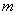

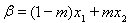

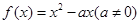 ,
,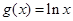 ,
,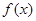 图象与
图象与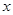 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为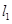 ,
,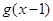 与
与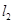 , 并且
, 并且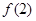 的值;
的值; 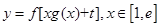 的最小值;
的最小值;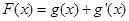 ,给定
,给定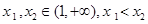 ,对于两个大于1的正数
,对于两个大于1的正数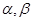 ,
,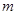 满足:
满足: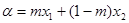 ,
,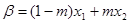 ,并且使得不等式
,并且使得不等式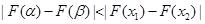 恒成立,求实数
恒成立,求实数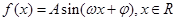 (其中
(其中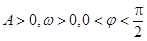 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为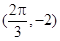 .
.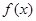 的解析式;
的解析式; 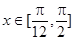 ,求
,求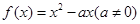 ,
,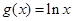 ,
,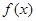 图象与
图象与 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为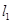 ,
,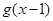 与
与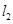 , 并且
, 并且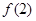 的值;
的值; 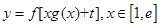 的最小值;
的最小值;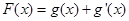 ,给定
,给定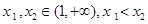 ,对于两个大于1的正数
,对于两个大于1的正数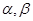 ,
,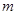 满足:
满足: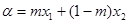 ,
,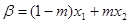 ,并且使得不等式
,并且使得不等式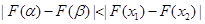 恒成立,求实数
恒成立,求实数