题目内容
(本小题满分12分)已知函数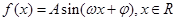 (其中
(其中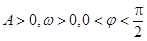 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为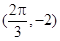 .
.
(1)求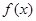 的解析式;
的解析式;
(2)当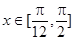 ,求
,求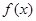 的值域.
的值域.
【答案】
(1)  ;(2)
;(2)  的值域为[-1,2].
的值域为[-1,2].
【解析】本试题主要是考查了但角函数的图像与性质的运用,以及三角函数解析式的求解和运用。
(1)由于最低点为 得A=2.
得A=2.
由x轴上相邻的两个交点之间的距离为 得
得 =
= ,即
,即 ,再代入点M可知参数初相的值,从而得到结论。
,再代入点M可知参数初相的值,从而得到结论。
(2)因为 ,然后利用三角函数的性质可知,函数的最值的求解。
,然后利用三角函数的性质可知,函数的最值的求解。
解(1)由最低点为 得A=2.
得A=2.
由x轴上相邻的两个交点之间的距离为 得
得 =
= ,即
,即 ,
,
由点 在图像上得
在图像上得 ,即
,即 ,
,
∴ ,得
,得 ,
,
又 ,∴
,∴ ,于是
,于是 ;
;
(2)∵ ,∴
,∴ ,
,
当 ,即
,即 时,
时, 取得最大值2;当
取得最大值2;当 ,即
,即 时,
时, 取得最小值-1,故
取得最小值-1,故 的值域为[-1,2].
的值域为[-1,2].

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目