题目内容
(本小题满分14分)
已知函数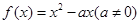 ,
,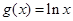 ,
,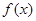 图象与
图象与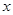 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为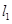 ,
,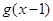 与
与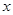 轴的交点N处的切线为
轴的交点N处的切线为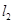 , 并且
, 并且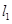 与
与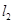 平行.
平行.
(1)求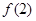 的值;
的值;
(2)已知实数t∈R,求函数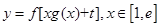 的最小值;
的最小值;
(3)令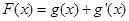 ,给定
,给定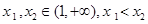 ,对于两个大于1的正数
,对于两个大于1的正数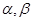 ,
,
存在实数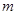 满足:
满足: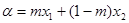 ,
,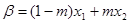 ,并且使得不等式
,并且使得不等式
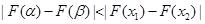 恒成立,求实数
恒成立,求实数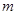 的取值范围.
的取值范围.
(1) ;
;
(2)①当 即
即 时,
时,
②当 即
即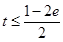 时,
时,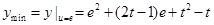
③当 即
即 时,
时,
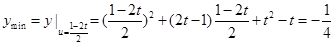 ;
;
 ,
,
【解析】本小题主要考查函数单调性的应用、利用导数研究曲线上某点切线方程、利用导数研究函数的单调性等基础知识,考查运算求解能力、化归与转化思想.属于中档题.
(1)利用导数的几何意义,分别求两函数在与两坐标轴的交点处的切线斜率,令其相等解方程即可得a值,从而得到f(2)的值;
(2)令u=xlnx,再研究二次函数u2+(2t-1)u+t2-t图象是对称轴u=  ,开口向上的抛物线,结合其性质求出最值;(3)先由题意得到F(x)=g(x)+g′(x)=lnx+
,开口向上的抛物线,结合其性质求出最值;(3)先由题意得到F(x)=g(x)+g′(x)=lnx+ 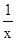 ,再利用导数工具研究所以F(x)在区间(1,+∞)上单调递增,得到当x≥1时,F(x)≥F(1)>0,下面对m进行分类讨论:①当m∈(0,1)时,②当m≤0时,③当m≥1时,结合不等式的性质即可求出a的取值范围.
,再利用导数工具研究所以F(x)在区间(1,+∞)上单调递增,得到当x≥1时,F(x)≥F(1)>0,下面对m进行分类讨论:①当m∈(0,1)时,②当m≤0时,③当m≥1时,结合不等式的性质即可求出a的取值范围.
解:  图象与
图象与 轴异于原点的交点
轴异于原点的交点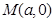 ,
,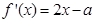
 图象与
图象与 轴的交点
轴的交点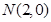 ,
,
由题意可得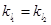 ,即
,即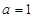 ,
………………………………………………2分
,
………………………………………………2分
∴ ,
, …………………………………………3分
…………………………………………3分
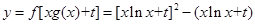 =
=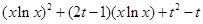 ………4分
………4分
令 ,在
,在  时,
时, ,
,
∴ 在
在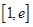 单调递增,
单调递增,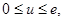 ………………5分
………………5分
 图象的对称轴
图象的对称轴 ,抛物线开口向上
,抛物线开口向上
①当 即
即 时,
时, …………………………………6分
…………………………………6分
②当 即
即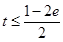 时,
时,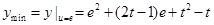 ………………………………7分
………………………………7分
③当 即
即 时,
时,
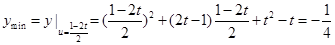 …………………8分
…………………8分
 ,
,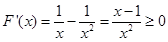

所以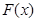 在区间
在区间 上单调递增 ………………………9分
上单调递增 ………………………9分
∴ 时,
时,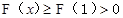
①当 时,有
时,有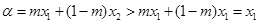 ,
,
 ,
,
得 ,同理
,同理 , …………………10分
, …………………10分
∴ 由 的单调性知
的单调性知 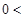
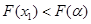 、
、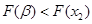
从而有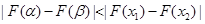 ,符合题设. ………………11分
,符合题设. ………………11分
②当 时,
时, ,
,
 ,
,
由 的单调性知
的单调性知 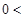
 ,
,
∴ ,与题设不符 ……………12分
,与题设不符 ……………12分
③当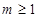 时,同理可得
时,同理可得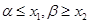 ,
,
得 ,与题设不符. ……………………13分
,与题设不符. ……………………13分
∴综合①、②、③得 ……………14分
……………14分
说明:各题如有其它解法,按照相应的步骤给分.

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)