题目内容
已知函数f(x)是定义在R上的奇函数,其最小正周期为3,且x∈(-
,0),f(x)=log2(-3x+1),则f(2014)= .
| 3 |
| 2 |
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:运用函数的周期性可得f(2014)=f(1),再由奇函数的定义,可得f(1)=-f(-1),结合已知区间的函数解析式,即可得到所求值.
解答:
解:函数f(x)是定义在R上的奇函数,其最小正周期为3,
则有f(-x)=-f(x),f(x+3)=f(x),
f(2014)=f(3×671+1)=f(1)=-f(-1),
由于x∈(-
,0),f(x)=log2(-3x+1),
则f(-1)=log2(3+1)=2,
故f(2014)=-2.
故答案为:-2.
则有f(-x)=-f(x),f(x+3)=f(x),
f(2014)=f(3×671+1)=f(1)=-f(-1),
由于x∈(-
| 3 |
| 2 |
则f(-1)=log2(3+1)=2,
故f(2014)=-2.
故答案为:-2.
点评:本题主要考查函数奇偶性和周期性的性质及运用,考查函数值的求法,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
已知等差数列{an}中,an=4n-3,则公差d的值为( )
| A、3 | B、1 | C、4 | D、2 |
已知f(x)=ln(x+1)-ln(1-x),x∈(-1,1),现有下列命题:
①f(-x)=-f(x);②f(
)=2f(x);③f(x)在(-1,1)上是增函数,
其中正确命题的序号是( )
①f(-x)=-f(x);②f(
| 2x |
| 1+x2 |
其中正确命题的序号是( )
| A、①②③ | B、②③ | C、①③ | D、①② |
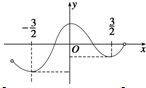
函数f(x)的图象如图所示,则最大、最小值分别为( )

A、f(
| ||||
B、f(0),f(
| ||||
C、f(0),f(-
| ||||
| D、f(0),f(3) |
下列图形中不可能是三棱柱在平面上的投影的是( )
A、 |
B、 |
C、 |
D、 |
