题目内容
5.椭圆$\frac{x^2}{3}+\frac{y^2}{2}=1$上一点P到左焦点的距离为$\frac{{\sqrt{3}}}{2}$,则P到右准线的距离为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{5\sqrt{5}}{10}$ | C. | $\frac{9}{2}$ | D. | $\frac{3}{2}$ |
分析 设P(x0,y0),由题意可得|PF1|=a+ex0=3,解得x0.再利用P到右准线的距离d=$\frac{{a}^{2}}{c}$-x0即可得出.
解答 解:设P(x0,y0),由椭圆$\frac{x^2}{3}+\frac{y^2}{2}=1$上一点P到左焦点F1的距离为$\frac{\sqrt{3}}{2}$,即|PF1|=a+ex0=$\frac{\sqrt{3}}{2}$,
∴a=$\sqrt{3}$,e=$\frac{\sqrt{3}}{3}$解得x0=-$\frac{3}{2}$.$\frac{{a}^{2}}{c}$=3,
∴P到右准线的距离d=3$+\frac{3}{2}$=$\frac{9}{2}$.
故选:C.
点评 本题考查了椭圆的标准方程及其性质,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
13.已知函数f(x)=(2x+1)ex+1+mx,若有且仅有两个整数使得f(x)≤0.则实数m的取值范围是( )
| A. | $({-\frac{3}{2},-\frac{3}{2e}})$ | B. | $[{-\frac{3}{2e},-\frac{5}{{3{e^2}}}})$ | C. | $[{-\frac{3}{2},-\frac{5}{{3{e^2}}}})$ | D. | $[{-2e,-\frac{3}{2e}})$ |
14.已知函数f(x)是奇函数,当x<0时,f(x)=-x2+x,若不等式f(x)-x≤2logax(a>0且a≠1)对?x∈(0,$\frac{\sqrt{2}}{2}$]恒成立,则实数a的取值范围是( )
| A. | (0,$\frac{1}{4}$] | B. | [$\frac{1}{4}$,1) | C. | (0,$\frac{1}{2}$] | D. | [$\frac{1}{4}$,$\frac{1}{2}$]∪(1,+∞) |
15.已知f(x)是定义在R上的奇函数,则f(0)=( )
| A. | 0 | B. | 1 | C. | -1 | D. | 不存在 |
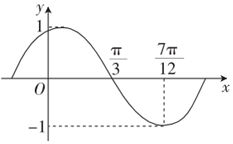 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.