题目内容
已知向量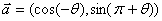 ,
,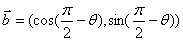 .
.
(Ⅰ)求证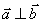 ;
;
(Ⅱ)若存在不等于0的实数k和t, 使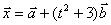 ,
,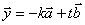 满足
满足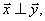 试求此时
试求此时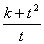 的最小值.
的最小值.
解:(Ⅰ)∵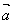 ·
· =cos(-
=cos(-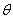 ) cos(
) cos(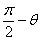 )+sin(
)+sin(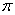 +
+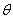 ) sin(
) sin(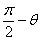 )
)
=sin cos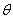 -sin
-sin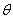 cos
cos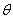
=0
∴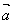 ⊥
⊥ .
.
(Ⅱ)由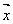 ⊥
⊥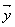 得
得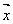 ·
·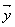 =0
=0
即[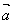 +(t2+3)
+(t2+3) ]·(-k
]·(-k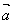 +t
+t )=0
)=0
∴-k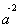 +(t3+3t)
+(t3+3t)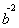 +[t-k(t2+3)]
+[t-k(t2+3)]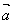 ·
· =0
=0
∴-k|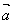 |2+(t3+3t)|
|2+(t3+3t)| |2=0
|2=0
又∵|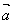 |2=1,|
|2=1,| |2=1
|2=1
∴-k+ t3+3t=0 ∴k=t3+3t
∴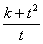 =
=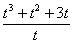
=t2+t+3
=(t+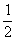 )2+
)2+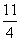
故当t=-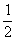 时,
时,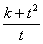 取得最小值,为
取得最小值,为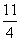 .
.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
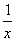 (x>0),以点(n,f(n))为切点作函数图象的切线ln(n∈N*),直线x=n+1与函数y=f(x)图象及切线ln分别相交于An,Bn,记an=|AnBn|.
(x>0),以点(n,f(n))为切点作函数图象的切线ln(n∈N*),直线x=n+1与函数y=f(x)图象及切线ln分别相交于An,Bn,记an=|AnBn|.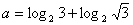 ,
,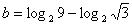 ,
, 则
则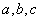 的大小关系是( )
的大小关系是( )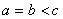 B.
B.  C.
C. 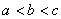 D.
D. 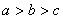
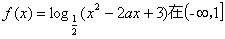 上是增函数,则实数
上是增函数,则实数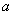 的取值范围是__________.
的取值范围是__________.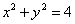 上,与直线4x+3y-12=0的距离最小的点的坐标为( )
上,与直线4x+3y-12=0的距离最小的点的坐标为( ) B.
B. 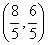 C.
C. 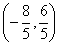 D.
D. 
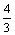 或a≥
或a≥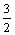 B、a≤-
B、a≤-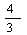 C、-
C、- ≤
≤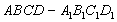 的棱长为1,
的棱长为1,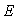 是
是 的中点,则
的中点,则 到平面
到平面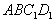 的距离是 (
的距离是 (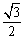 B.
B. C.
C. 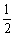 D.
D. 
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,若
,若 是
是 的等比中项,
的等比中项, 是
是 与
与 的等差中项,则椭圆的离心率是
的等差中项,则椭圆的离心率是 B.
B. C.
C. D.
D.