题目内容
已知函数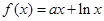 ,其中
,其中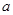 为常数,
为常数,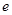 为自然对数的底数.
为自然对数的底数.
(1)求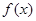 的单调区间;
的单调区间;
(2)若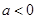 ,且
,且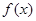 在区间
在区间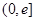 上的最大值为
上的最大值为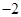 ,求
,求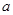 的值;
的值;
(3)当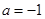 时,试证明:
时,试证明: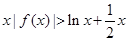 .
.
【答案】
(1)单调增区间为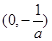 ,单调减区间为
,单调减区间为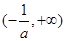 ;(2)
;(2)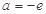 ;(3)证明过程详见解析.
;(3)证明过程详见解析.
【解析】
试题分析:本题主要考查导数的运算,利用导数研究函数的单调性、最值、不等式等基础知识,考查函数思想、分类讨论思想,考查综合分析和解决问题的能力.第一问,讨论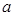 的正负来求单调性,利用导数大于0或小于0,通过解不等式来求函数的单调性;第二问,讨论
的正负来求单调性,利用导数大于0或小于0,通过解不等式来求函数的单调性;第二问,讨论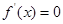 方程的根与已知区间的关系,先判断函数的单调性,再求最值,列出方程解出
方程的根与已知区间的关系,先判断函数的单调性,再求最值,列出方程解出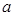 的值;第三问,证明“
的值;第三问,证明“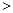 ”两边的两个函数的最值,来证明大小关系.
”两边的两个函数的最值,来证明大小关系.
试题解析:(1)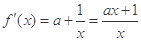 1分
1分
当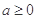 时,
时,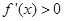 恒成立,故
恒成立,故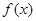 的单调增区间为
的单调增区间为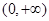 3分
3分
当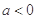 时,令
时,令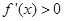 解得
解得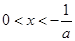 ,令
,令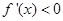 解得
解得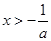 ,故
,故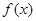 的单调增区间为
的单调增区间为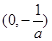 ,
,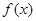 的单调减区间为
的单调减区间为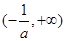 5分
5分
(2)由(I)知,
①当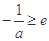 ,即
,即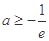 时,
时,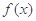 在
在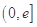 上单调递增,∴
上单调递增,∴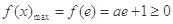 舍; 7分
舍; 7分
②当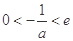 ,即
,即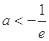 时,
时,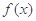 在
在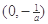 上递增,在
上递增,在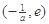 上递减,
上递减,
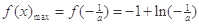 ,令
,令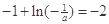 ,得
,得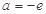 9分
9分
(Ⅲ)即要证明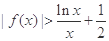 ,
10分
,
10分
由(Ⅰ)知当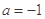 时,
时,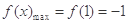 ,∴
,∴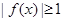 , 11分
, 11分
又令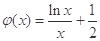 ,
,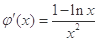 ,
12分
,
12分
故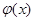 在
在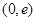 上单调递增,在
上单调递增,在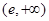 上单调递减,
13分
上单调递减,
13分
故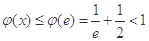 14分
14分
即证明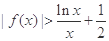 .
.
考点:1.利用导数判断函数的单调性;2.利用导数求函数最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
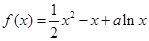 (其中
(其中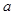 为常数).
为常数).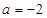 时,求函数
时,求函数 的最值;
的最值; (其中
(其中 为常数).
为常数). 时,求函数的单调区间;
时,求函数的单调区间;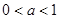 时,设函数
时,设函数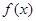 的3个极值点为
的3个极值点为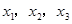 ,且
,且 .证明:
.证明: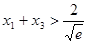 .
. ,其中
,其中 为常数,且
为常数,且
 是奇函数,求
是奇函数,求 时,设
时,设 ,且函数
,且函数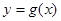 的图像与
的图像与 的图像关于
的图像关于 对称,求
对称,求 的取值集合B;
的取值集合B; 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 时,不等式
时,不等式