题目内容
(本题满分16分,第1小题5分,第2小题6分,第3小题5分)
已知函数 ,其中
,其中 为常数,且
为常数,且
(1)若 是奇函数,求
是奇函数,求 的取值集合A;
的取值集合A;
(2)(理)当 时,设
时,设 的反函数为
的反函数为 ,且函数
,且函数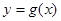 的图像与
的图像与 的图像关于
的图像关于 对称,求
对称,求 的取值集合B;
的取值集合B;
(文)当 时,求
时,求 的反函数;
的反函数;
(3)(理)对于问题(1)(2)中的A、B,当 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。
(文)对于问题(1)中的A,当 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。
【答案】
(1)
(2)(理)B={—4}
(文)
(3)(理)x的取值范围为{1,4}
(文)x的取值范围为{1,4}
【解析】解:(1)由必要条件 ,
,
所以 , ………………2分
, ………………2分
下面证充分性,当 ,
,
任取

 =0恒成立……………………2分
=0恒成立……………………2分
由 ……………………1分
……………………1分
(2)(理)当
得
互换x,y得 ………………1分
………………1分
从而
所以 ……………………2分
……………………2分
即B={—4} ……………………1分
(文)当a=1时,
其值域是 ……………………3分
……………………3分
得 互换x,y
互换x,y
得 ……………………3分
……………………3分
(3)(理)原问题转化为

 恒成立
恒成立
则 ……………………2分
……………………2分
或
则x的取值范围为{1,4}……………………2分
(文)原问题转化为
 ,
,
 恒成立
恒成立
则 ……………………2分
……………………2分
或
则x的取值范围为{1,4}……………………2分

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,
,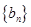 是等差数列,且
是等差数列,且 ,求非零常数
,求非零常数 ;
; ,求证:
,求证: .
. 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若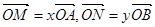 。
。 与
与 的关系为
的关系为 ;
; ,定义在
,定义在 上的偶函数
上的偶函数 ,当
,当 时
时 ,且函数
,且函数 对称,求证:
对称,求证: ,并求
,并求 时的解析式;
时的解析式; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。 、
、 为坐标平面
为坐标平面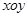 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点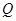 (异于
(异于 ,点
,点 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
; 在椭圆
在椭圆 上,试问:点
上,试问:点 、
、 是圆
是圆 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 是
是 轴正方向的单位向量,设
轴正方向的单位向量,设 =
= ,
,  =
= ,且满足
,且满足 .
.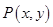 的轨迹方程;
的轨迹方程; 的直线
的直线 交上述轨迹于
交上述轨迹于 两点,且
两点,且 ,求直线
,求直线