题目内容
已知函数 (其中
(其中 为常数).
为常数).
(Ⅰ)当 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)当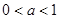 时,设函数
时,设函数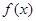 的3个极值点为
的3个极值点为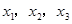 ,且
,且 .证明:
.证明: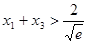 .
.
(Ⅰ)单调减区间为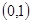 ,
, ;增区间为
;增区间为 .(Ⅱ)详见解析.
.(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)将 代入
代入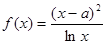 ,然后求导便可得其单调区间.
,然后求导便可得其单调区间.
(Ⅱ)我们分以下几步来分析.
第一步、对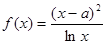 求导得:
求导得: .显然
.显然 是它的一个极值点,下面我们要弄清楚
是它的一个极值点,下面我们要弄清楚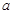 应该是
应该是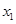 还是
还是 .另两个极值点便是方程
.另两个极值点便是方程 的根.对这个方程,我们不可能直接解,所以接下来就利用导数研究函数
的根.对这个方程,我们不可能直接解,所以接下来就利用导数研究函数 .
.
第二步、对 求导得:
求导得:
∴函数 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增
当 时,
时,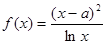
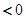 ,
, .又
.又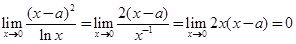 ,
,
所以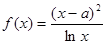 在
在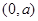 上必有一个极值点.
上必有一个极值点.
因为 ,所以
,所以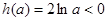 ,
, ,
,
∴ 的两个零点必有一个小于
的两个零点必有一个小于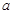 (实际上比
(实际上比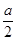 还小),而另一个大于1,
还小),而另一个大于1,
∴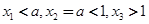 .
.
∴当 时,
时, 是函数
是函数 的两个零点,且
的两个零点,且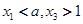 .
.
即有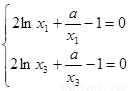 .这样问题转化为在该条件下证明
.这样问题转化为在该条件下证明 .那么这个不等式如何证呢?
.那么这个不等式如何证呢?
第三步、注意到待证不等式 中不含
中不含 ,故考虑消去
,故考虑消去 ,找到
,找到 之间的关系式.
之间的关系式.
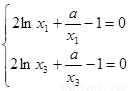 消去
消去 有
有 .
.
令 ,
, 有零点
有零点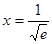 .
.
∴函数 在
在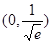 上递减,在
上递减,在 上递增,
上递增, 在
在 处取得极小值.由于
处取得极小值.由于 ,所以
,所以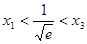 .
.
因为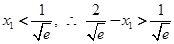 .
.
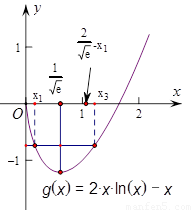
所以要证明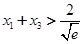 ,只需证
,只需证 .那么这个不等式又如何证明呢?
.那么这个不等式又如何证明呢?
因为函数 在
在 上递增,所以转化为证
上递增,所以转化为证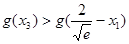 .
.
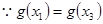
 即证
即证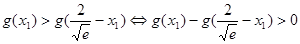 .
.
这个不等式,通过构造函数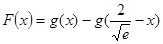 ,再利用导数就很容易证明了.
,再利用导数就很容易证明了.
试题解析:(Ⅰ)求导得: .
.
令 可得
可得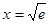 .列表如下:
.列表如下:
|
|
|
|
|
|
|
|
- |
- |
0 |
+ |
|
|
减 |
减 |
极小值 |
增 |
单调减区间为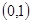 ,
, ;增区间为
;增区间为 .
5分
.
5分
(Ⅱ)由题,
对于函数 ,有
,有
∴函数 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增
∵函数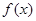 有3个极值点
有3个极值点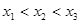 ,
,
从而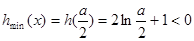 ,所以
,所以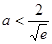 ,
,
当 时,
时,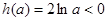 ,
, ,
,
∴ 函数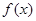 的递增区间有
的递增区间有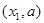 和
和 ,递减区间有
,递减区间有 ,
, ,
, ,
,
此时,函数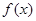 有3个极值点,且
有3个极值点,且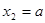 ;
;
∴当 时,
时, 是函数
是函数 的两个零点, 9分
的两个零点, 9分
即有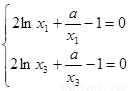 ,消去
,消去 有
有
令 ,
, 有零点
有零点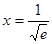 ,且
,且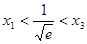
∴函数 在
在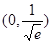 上递减,在
上递减,在 上递增
上递增
要证明




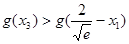
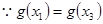
 即证
即证
构造函数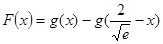 ,
,
 ,所以
,所以
只需要证明 单调递减即可.而
单调递减即可.而 ,
,
 在
在 上单调递增,
上单调递增, 
∴当 时,
时, .
14分
.
14分
考点:1、导数的应用;2、不等式的证明.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案



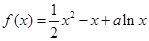 (其中
(其中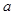 为常数).
为常数).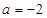 时,求函数
时,求函数 的最值;
的最值; ,其中
,其中 为常数,且
为常数,且
 是奇函数,求
是奇函数,求 时,设
时,设 ,且函数
,且函数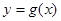 的图像与
的图像与 的图像关于
的图像关于 对称,求
对称,求 的取值集合B;
的取值集合B; 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 时,不等式
时,不等式