题目内容
若双曲线C1与椭圆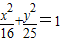
有相同的焦点，与双曲线C2：
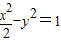有相同渐近线．（1）求C2的实轴长和渐近线方程；
（2）求C1的方程．
【答案】分析：（1）由题意可得C2中：a=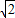
，b=1，进而可得所求；
（2）法一：设所求的双曲线的方程为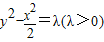
，由题意可得关于λ的方程，解之可得；
法二：设C1：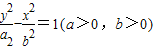
，可得
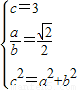，解之可得a，b，可得方程．
解答：解：（1）由题意可得C2中：a=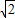
，b=1，
故实轴长为2a=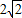
，渐近线方程
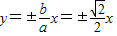；…（5分）
（2）法一：依题意可设所求的双曲线的方程为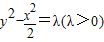
…（6分）
即
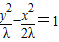…（7分）
又∵双曲线与椭圆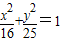
有相同的焦点，
∴λ+2λ=25-16=9解得λ=3…（11分）
∴C1的标准方程为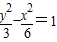
…（13分）
法二：设C1：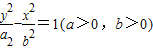
，…（6分）
可得
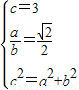求得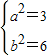 
…（11分）
∴C1的标准方程为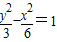
…（13分）
点评：本题考查双曲线与椭圆的简单性质，涉及圆锥曲线的基本运算，属中档题．
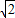，b=1，进而可得所求；（2）法一：设所求的双曲线的方程为
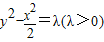，由题意可得关于λ的方程，解之可得；法二：设C1：
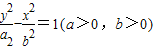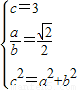，可得，解之可得a，b，可得方程．解答：解：（1）由题意可得C2中：a=
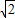，b=1，故实轴长为2a=
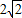，渐近线方程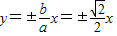；…（5分）（2）法一：依题意可设所求的双曲线的方程为
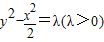…（6分）即
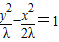…（7分）又∵双曲线与椭圆
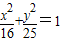有相同的焦点，∴λ+2λ=25-16=9解得λ=3…（11分）
∴C1的标准方程为
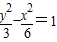…（13分）法二：设C1：
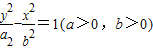，…（6分）可得
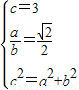求得 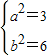…（11分）∴C1的标准方程为
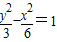…（13分）点评：本题考查双曲线与椭圆的简单性质，涉及圆锥曲线的基本运算，属中档题．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
已知椭圆C1的中心在原点，离心率为
，焦点在x轴上且长轴长为10．过双曲线C2：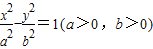
右焦点F2作垂直于x轴的直线交双曲线C2于M、N两点．