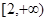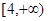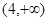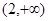题目内容
已知椭圆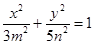 和双曲线
和双曲线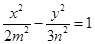 有公共的焦点,那么双曲线的渐近线方程为
有公共的焦点,那么双曲线的渐近线方程为
A.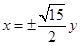 | B.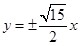 | C.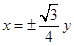 | D.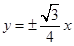 |
D
解析试题分析:因为焦点相同所以有 ,解得
,解得 ,即
,即 。
。
双曲线的渐近线方程为 ,即
,即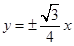 ,故D正确。
,故D正确。
考点:椭圆,双曲线及双曲线的渐近线

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
已知圆 的圆心为抛物线
的圆心为抛物线 的焦点,直线
的焦点,直线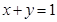 与圆
与圆 相切,则该圆的方程为( )
相切,则该圆的方程为( )
A.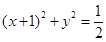 | B.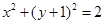 |
C.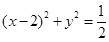 | D. |
过双曲线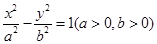 的左焦点
的左焦点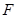 作圆
作圆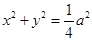 的切线,切点为
的切线,切点为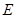 ,直线
,直线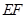 交双曲线右支于点
交双曲线右支于点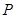 ,若
,若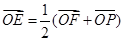 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.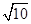 | B.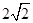 | C.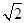 | D.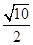 |
平面上动点 满足
满足 ,
, ,
, ,则一定有( )
,则一定有( )
A. | B. |
C. | D. |
已知抛物线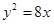 的焦点与双曲线
的焦点与双曲线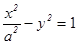 的一个焦点重合,则该双曲线的离心率为( )
的一个焦点重合,则该双曲线的离心率为( )
A.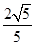 | B.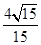 | C. | D.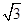 |
已知F为抛物线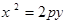
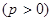 的焦点,M为其上一点,且
的焦点,M为其上一点,且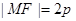 ,则直线MF的斜率为( ).
,则直线MF的斜率为( ).
A.-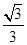 | B.±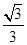 | C.-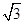 | D.±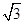 |
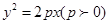 ,过其焦点且斜率为1的直线交抛物线与A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为( )
,过其焦点且斜率为1的直线交抛物线与A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为( )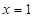 B.
B.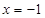 C.
C.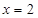 D.
D.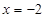
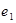 、
、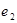 ,则下列关于
,则下列关于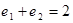 B.
B.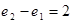 C.
C.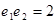 D.
D.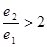
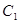 与双曲线
与双曲线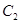 有共同的焦点
有共同的焦点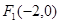 ,
,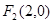 ,椭圆的一个短轴端点为
,椭圆的一个短轴端点为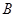 ,直线
,直线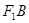 与双曲线的一条渐近线平行,椭圆
与双曲线的一条渐近线平行,椭圆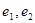 ,则
,则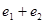 取值范围为( )
取值范围为( )