题目内容
在△ABC中.Sin2A≤sin2B+sin2C-sinBsinC.则A的取值范围是 ( )
A.(0,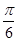 ] B.[
] B.[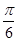 ,
,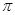 )
)
C.(0,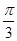 ] D.[
] D.[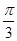 ,
,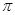 )
)
A.(0,
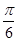 ] B.[
] B.[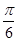 ,
,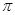 )
)C.(0,
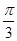 ] D.[
] D.[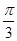 ,
,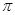 )
)C
由题意及正弦定理得
a2≤b2+c2-bc bc≤b2+c2-a2
bc≤b2+c2-a2
 ≥1
≥1
又由余弦定理知2cosA= ≥1
≥1 cosA≥
cosA≥
因为角A为三角形内角,所以0<A≤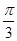
a2≤b2+c2-bc
 bc≤b2+c2-a2
bc≤b2+c2-a2
 ≥1
≥1又由余弦定理知2cosA=
 ≥1
≥1 cosA≥
cosA≥
因为角A为三角形内角,所以0<A≤
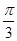

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 .
. 的长
的长  是
是 的中点,求中线
的中点,求中线 的长度.
的长度.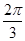
 ,求
,求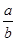 的值.
的值. 中,若
中,若 ,则
,则 ( )
( )

 或
或
 ,若
,若 ,则△ABC的面积等于__________。
,则△ABC的面积等于__________。 =
= ,
, =2,B=45°,则角A=( )
=2,B=45°,则角A=( ) 或
或
 或
或
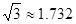 )
)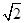 ,BC=a的△ABC有两个,那么a的取值范围是 ( )
,BC=a的△ABC有两个,那么a的取值范围是 ( )