题目内容
若 展开式中含x的项的系数为280,则a=
展开式中含x的项的系数为280,则a=
- A.-2
- B.2
- C.

- D.

C
分析:在二项展开式的通项公式中,令x的幂指数等于1,求出r的值,即可求得展开式中含x的项的系数,再根据展开式中含x的项的系数等于280,求得a的值.
解答:由于 展开式的通项公式为 Tr+1=
展开式的通项公式为 Tr+1=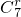 •x7-r•(-1)r•(ax)-r=(-1)r•
•x7-r•(-1)r•(ax)-r=(-1)r•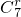 •a-r•x7-2r.
•a-r•x7-2r.
令7-2r=1,r=3,故展开式中含x的项的系数为(-1)3• •a-3=280,∴a=-
•a-3=280,∴a=- ,
,
故选C.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于中档题.
分析:在二项展开式的通项公式中,令x的幂指数等于1,求出r的值,即可求得展开式中含x的项的系数,再根据展开式中含x的项的系数等于280,求得a的值.
解答:由于
 展开式的通项公式为 Tr+1=
展开式的通项公式为 Tr+1=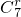 •x7-r•(-1)r•(ax)-r=(-1)r•
•x7-r•(-1)r•(ax)-r=(-1)r•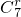 •a-r•x7-2r.
•a-r•x7-2r.令7-2r=1,r=3,故展开式中含x的项的系数为(-1)3•
 •a-3=280,∴a=-
•a-3=280,∴a=- ,
,故选C.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
相关题目
 ,则二项式
,则二项式 展开式中含x的项的系数是 .
展开式中含x的项的系数是 . 展开式中含x的项是第六项,则其展开式的项数是_ .
展开式中含x的项是第六项,则其展开式的项数是_ .