题目内容
如图,已知![]()
求证:存在不全为0的实数l、m、n,当la+mb+nc=0,且l+m+n=0时,A、B、C三点在一条直线上.

答案:
解析:
提示:
解析:
|
证明:由l+m+n=0得l=-m-n,代入la+mb+nc=0得:m(b-a)+n(c-a)=0,m 所以 |
提示:
|
要证A、B、C三点共线,只要证明 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



































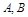 分别是椭圆
分别是椭圆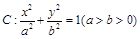 的左、右顶点,点
的左、右顶点,点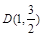 在椭圆
在椭圆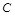 上,且直线
上,且直线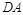 与直线
与直线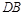 的斜率之积为
的斜率之积为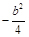 .
.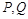 是椭圆
是椭圆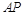 与
与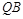 交于点
交于点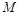 ,直线
,直线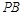 与
与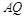 交于点
交于点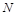 .①
求证:
.①
求证: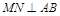 ;② 若弦
;② 若弦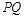 过椭圆的右焦点
过椭圆的右焦点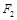 ,求直线
,求直线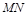 的方程.
的方程.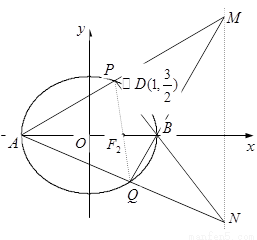
 求证:a∥l.
求证:a∥l.