题目内容
如图,已知 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且 ,
, .
.

(1)求证:平面 //平面
//平面 ;
;
(2)若 平面
平面 ,且
,且 ,
, ,
, ,求证:
,求证: 平面
平面 ;
;
(3)在(2)的条件下,设点 为
为 上的动点,求当
上的动点,求当 取得最小值时
取得最小值时 的长.
的长.
【答案】
(1)详见解析;(2)详见解析;(3) .
.
【解析】
试题分析:(1)通过证明平行四边形分别证明 和
和 ,利用直线与平面平行的判定定理得到
,利用直线与平面平行的判定定理得到 平面
平面 和
和 平面
平面 ,最后利用平面与平面平行的判定定理证明平面
,最后利用平面与平面平行的判定定理证明平面 平面
平面 ;(2)先证明
;(2)先证明 平面
平面 ,于是得到
,于是得到 ,由
,由 再由四边形
再由四边形 为正方形得到
为正方形得到 ,最后利用直线与平面垂直的判定定理证明
,最后利用直线与平面垂直的判定定理证明 平面
平面 ;(3)将三棱柱
;(3)将三棱柱
 的侧面沿着
的侧面沿着 展开,利用
展开,利用 、
、 、
、 三点共线求出
三点共线求出 的最小值,并利用相似三角形求出
的最小值,并利用相似三角形求出 的长度.
的长度.
试题解析:(1)证明: 且
且 ,
, 四边形
四边形 是平行四边形,
是平行四边形, ,
,
 面
面 ,
,
 面
面
 平面
平面 ,
,
同理可得 平面
平面 ,又
,又 ,
, 平面
平面 平面
平面 ;
;
(2) 平面
平面 ,
, 平面
平面 ,
, 平面
平面
 平面
平面 ,
,
平面
 平面
平面 ,
,

 ,
, ,
, ,
, ,
, ,
, 平面
平面 ,
,
 ,
, ,
, ,
,
又 ,
, 得
得 为正方形,
为正方形, ,
,
又 ,
, 平面
平面 ;
;
(3)将三棱柱 的侧面
的侧面 绕侧棱
绕侧棱 旋转到与侧面
旋转到与侧面 在同一平面内如下图示,连结
在同一平面内如下图示,连结 交
交 于点
于点 ,则由平面几何的知识知,这时
,则由平面几何的知识知,这时 取得最小值,
取得最小值,
 ,
, .
.

考点:1.平面与平面平行;2.直线与平面垂直;3.空间几何体的侧面展开图

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图,已知棱长为1的正方体ABCD-A1B1C1D1.
如图,已知棱长为1的正方体ABCD-A1B1C1D1.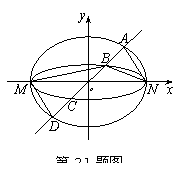
















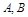 分别是椭圆
分别是椭圆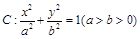 的左、右顶点,点
的左、右顶点,点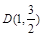 在椭圆
在椭圆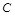 上,且直线
上,且直线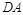 与直线
与直线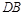 的斜率之积为
的斜率之积为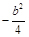 .
.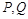 是椭圆
是椭圆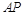 与
与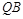 交于点
交于点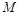 ,直线
,直线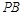 与
与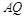 交于点
交于点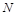 .①
求证:
.①
求证: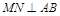 ;② 若弦
;② 若弦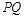 过椭圆的右焦点
过椭圆的右焦点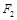 ,求直线
,求直线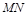 的方程.
的方程.