题目内容
如图,已知 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且 ,
, .
.

(1)求证:平面 //平面
//平面 ;
;
(2)若 平面
平面 ,且
,且 ,
, ,
, ,求证:
,求证: 平面
平面 ;
;
(3)在(2)的条件下,求二面角 的余弦值.
的余弦值.
【答案】
(1)详见解析;(2)详见解析:(3) .
.
【解析】
试题分析:(1)通过证明平行四边形分别证明 和
和 ,利用直线与平面平行的判定定理得到
,利用直线与平面平行的判定定理得到 平面
平面 和
和 平面
平面 ,最后利用平面与平面平行的判定定理证明平面
,最后利用平面与平面平行的判定定理证明平面 平面
平面 ;(2)证法1是先证明
;(2)证法1是先证明 平面
平面 ,于是得到
,于是得到 ,由
,由 再由四边形
再由四边形 为正方形得到
为正方形得到 ,最后利用直线与平面垂直的判定定理证明
,最后利用直线与平面垂直的判定定理证明 平面
平面 ;证法2是建立以以点
;证法2是建立以以点 为原点,分别以
为原点,分别以 、
、 、
、 所在的直线为
所在的直线为 、
、 、
、 轴的空间直角坐标系,利用空间向量法来证明
轴的空间直角坐标系,利用空间向量法来证明 平面
平面 ;(3)在(2)的基础上利用空间向量法求出二面角
;(3)在(2)的基础上利用空间向量法求出二面角 的余弦值.
的余弦值.
试题解析:(1)证明: 且
且 ,
, 四边形
四边形 是平行四边形,
是平行四边形, ,
,
 面
面 ,
,
 面
面
 平面
平面 ,
,
同理可得 平面
平面 ,又
,又 ,
, 平面
平面 平面
平面 ;
;
(2)证法1: 平面
平面 ,
, 平面
平面 ,
, 平面
平面
 平面
平面 ,
,
平面
 平面
平面 ,
,

 ,
, ,
, ,
, ,
, ,
, 平面
平面 ,
,
 ,
, ,
, ,
,
又 ,
, 得
得 为正方形,
为正方形, ,
,
又 ,
, 平面
平面 ;
;
证法2: ,
, ,
, ,
, ,
, ,
,
 平面
平面 ,
, ,
, 平面
平面 ,
,
以点 为原点,分别以
为原点,分别以 、
、 、
、 所在的直线为
所在的直线为 、
、 、
、 轴建立空间直角坐标系如图示,由已知可
轴建立空间直角坐标系如图示,由已知可 、
、 、
、 、
、 、
、 、
、 ,
,
则 ,
, ,
, ,
,
 ,
, ,
, ,
, ,
,
又 ,
, 平面
平面 .
.

(3)由(2)得 ,
, ,
,
设平面 的法向量
的法向量 ,则由
,则由 ,
, 得
得 ,
,
令 得
得 ,
,
由(2)知 是平面
是平面 的法向量,
的法向量, ,
,
即二面角 的余弦值为
的余弦值为 .
.
(其它解法请参照给分)
考点:1.平面与平面平行;2.直线与平面垂直;3.二面角;4.空间向量法

练习册系列答案
相关题目
 如图,已知棱长为1的正方体ABCD-A1B1C1D1.
如图,已知棱长为1的正方体ABCD-A1B1C1D1.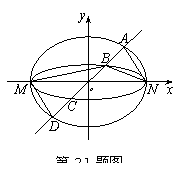



















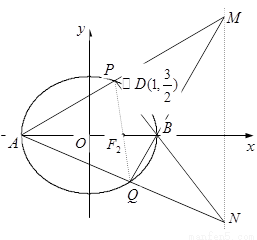
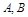 分别是椭圆
分别是椭圆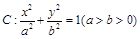 的左、右顶点,点
的左、右顶点,点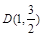 在椭圆
在椭圆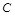 上,且直线
上,且直线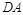 与直线
与直线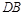 的斜率之积为
的斜率之积为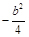 .
.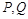 是椭圆
是椭圆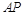 与
与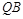 交于点
交于点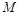 ,直线
,直线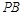 与
与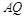 交于点
交于点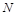 .①
求证:
.①
求证: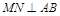 ;② 若弦
;② 若弦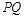 过椭圆的右焦点
过椭圆的右焦点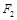 ,求直线
,求直线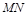 的方程.
的方程.