题目内容
【题目】已知函数![]() ,
, ![]() ,
, ![]()
(1)若![]() ,且
,且![]() 在其定义域上存在单调递减区间,求实数
在其定义域上存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,
, ![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() 、
、![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的垂线分别交
轴的垂线分别交![]() ,
, ![]() 于点
于点![]() 、
、![]() ,证明:
,证明: ![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线不平行.
处的切线不平行.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】分析:第一问将![]() 代入,求得
代入,求得![]() 的解析式,函数在定义域上存在单调递减区间,等价于导数
的解析式,函数在定义域上存在单调递减区间,等价于导数![]() 有正解,结合二次函数图像求得结果,第二问恒成立转化为求函数最值来处理,第三问假设存在,最后推出矛盾,从而得结果.
有正解,结合二次函数图像求得结果,第二问恒成立转化为求函数最值来处理,第三问假设存在,最后推出矛盾,从而得结果.
详解:(1)![]() ,
, ![]()
则![]()
因为函数![]() 存在单调递减区间,所以
存在单调递减区间,所以![]() 有正解.
有正解.
法1:因![]() 为开口向上的抛物线且过点
为开口向上的抛物线且过点![]()
∴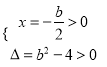 ,∴
,∴![]() ,∴
,∴![]()
法2: ![]() 有正解,∴
有正解,∴![]() ,∴
,∴![]()
(2)![]()
∴![]()
![]() .
.
令![]() ,
, ![]() ,于是
,于是![]()
当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 是减函数,
是减函数,
当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 是增函数.
是增函数.
所以![]() 在
在![]() 时取得最小值,
时取得最小值, ![]() ,
,
因为![]() 恒成立,所以
恒成立,所以![]() ,
,
因![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
令![]() ,易知
,易知![]() 关于
关于![]() 在
在![]() 上单调递增,又
上单调递增,又![]()
![]() ,∴
,∴![]() .
.
(3)证法一.设点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() ,
, ![]() ,不妨设
,不妨设![]() .
.
则点![]() 、
、![]() 的横坐标为
的横坐标为![]() ,
,
![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]()
![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
假设![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线平行,则
处的切线平行,则![]() .
.
即![]() ,则
,则
![]()
![]()
![]()
所以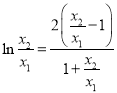 .设
.设![]() ,则
,则![]() ,
, ![]() .①
.①
令![]() ,
, ![]() .则
.则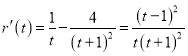 .
.
因为![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,故
上单调递增,故![]() .
.
则![]() .这与①矛盾,假设不成立.
.这与①矛盾,假设不成立.
故![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线不平行.
处的切线不平行.
证法二:同证法一得![]() .
.
因为![]() ,所以
,所以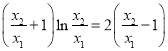 .
.
令![]() ,得
,得![]() ,
, ![]() .②
.②
令![]() ,
, ![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() 时,
时, ![]() .
.
故![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() ,即
,即![]() .
.
于是![]() 在
在![]() 上单调递增.
上单调递增.
故![]() ,即
,即![]() .这与②矛盾,假设不成立.
.这与②矛盾,假设不成立.
故点![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线不平行.
处的切线不平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目