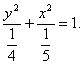题目内容
求经过两点P1(
解法一:因为焦点位置不确定,故可考虑两种情形.
(1)焦点在x轴上时:
设椭圆的方程为![]() =1(a>b>0).
=1(a>b>0).
依题意知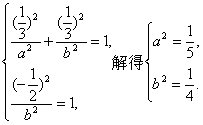
∵![]() ,∴方程组无解.
,∴方程组无解.
(2)焦点在y轴上时:
设椭圆的方程为![]() =1(a>b>0).
=1(a>b>0).
依题意可得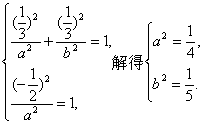
∴所求椭圆的标准方程为![]()
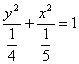
解法二:设所求椭圆方程的一般式为Ax2+By2=1(A>0,B>0).
依题意可得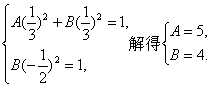
∴所求椭圆的方程为5x2+4y2=1.
∴标准方程为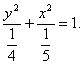

练习册系列答案
相关题目
题目内容
求经过两点P1(
解法一:因为焦点位置不确定,故可考虑两种情形.
(1)焦点在x轴上时:
设椭圆的方程为![]() =1(a>b>0).
=1(a>b>0).
依题意知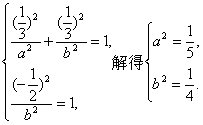
∵![]() ,∴方程组无解.
,∴方程组无解.
(2)焦点在y轴上时:
设椭圆的方程为![]() =1(a>b>0).
=1(a>b>0).
依题意可得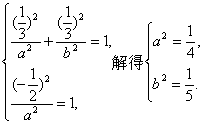
∴所求椭圆的标准方程为![]()
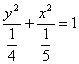
解法二:设所求椭圆方程的一般式为Ax2+By2=1(A>0,B>0).
依题意可得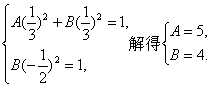
∴所求椭圆的方程为5x2+4y2=1.
∴标准方程为